题目内容
设函数f(x)=xekx(k≠0),(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)讨论函数f(x)的单调性;
(3)设g(x)=x2-2bx+4,当k=1时,若对任意x1∈R,存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.
【答案】分析:(1)f′(x)=(1+kx)ekx,由f(0)=0,且f′(0)=1,能求出曲线y=f(x)在点(0,f(0))处的切线方程.
(2)令f′(x)=(1+kx)ekx>0,所以1+kx>0,由此利用k的符号进行分类讨论,能求出f(x)的单调性.
(3)当k=1时,f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,所以对任意x1∈R,有f(x1)≥f(-1)=-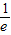 ,已知存在x2∈[1,2],使f(x1)≥g(x2),所以-
,已知存在x2∈[1,2],使f(x1)≥g(x2),所以-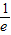 ≥g(x2),x2∈[1,2],由此能求出实数b取值范围.
≥g(x2),x2∈[1,2],由此能求出实数b取值范围.
解答:解:(1)f′(x)=(1+kx)ekx,
因为f(0)=0,且f′(0)=1,
所以曲线y=f(x)在点(0,f(0))处的切线方程为:y=x.(4分)
(2)令f′(x)=(1+kx)ekx>0,所以1+kx>0,
当k>0时,x>-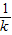 ,
,
此时f(x)在(-∞,-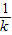 )上单调递减,在(-
)上单调递减,在(-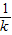 ,+∞)上单调递增;
,+∞)上单调递增;
当k<0时,x<-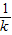 ,
,
此时f(x)在(-∞,-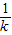 )上单调递增,在(-
)上单调递增,在(-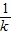 ,+∞)上单调递减.(8分)
,+∞)上单调递减.(8分)
(3)当k=1时,f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,
所以对任意x1∈R,有f(x1)≥f(-1)=-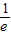 ,
,
又已知存在x2∈[1,2],
使f(x1)≥g(x2),所以-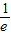 ≥g(x2),x2∈[1,2],
≥g(x2),x2∈[1,2],
即存在x∈[1,2],使g(x)=x2-2bx+4≤-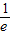 ,
,
即2b≥x+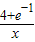 ,
,
即因为当x∈[1,2],x+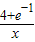 ∈[4+
∈[4+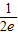 ,5+
,5+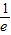 ],
],
所以2b≥4+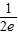 ,即实数b取值范围是b≥
,即实数b取值范围是b≥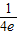 .(14分)
.(14分)
点评:本题考查切线方程的求法,考查函数单调性的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答.
(2)令f′(x)=(1+kx)ekx>0,所以1+kx>0,由此利用k的符号进行分类讨论,能求出f(x)的单调性.
(3)当k=1时,f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,所以对任意x1∈R,有f(x1)≥f(-1)=-
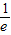 ,已知存在x2∈[1,2],使f(x1)≥g(x2),所以-
,已知存在x2∈[1,2],使f(x1)≥g(x2),所以-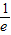 ≥g(x2),x2∈[1,2],由此能求出实数b取值范围.
≥g(x2),x2∈[1,2],由此能求出实数b取值范围.解答:解:(1)f′(x)=(1+kx)ekx,
因为f(0)=0,且f′(0)=1,
所以曲线y=f(x)在点(0,f(0))处的切线方程为:y=x.(4分)
(2)令f′(x)=(1+kx)ekx>0,所以1+kx>0,
当k>0时,x>-
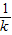 ,
,此时f(x)在(-∞,-
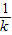 )上单调递减,在(-
)上单调递减,在(-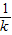 ,+∞)上单调递增;
,+∞)上单调递增;当k<0时,x<-
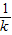 ,
,此时f(x)在(-∞,-
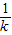 )上单调递增,在(-
)上单调递增,在(-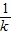 ,+∞)上单调递减.(8分)
,+∞)上单调递减.(8分)(3)当k=1时,f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,
所以对任意x1∈R,有f(x1)≥f(-1)=-
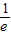 ,
,又已知存在x2∈[1,2],
使f(x1)≥g(x2),所以-
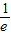 ≥g(x2),x2∈[1,2],
≥g(x2),x2∈[1,2],即存在x∈[1,2],使g(x)=x2-2bx+4≤-
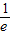 ,
,即2b≥x+
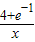 ,
,即因为当x∈[1,2],x+
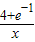 ∈[4+
∈[4+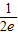 ,5+
,5+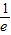 ],
],所以2b≥4+
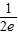 ,即实数b取值范围是b≥
,即实数b取值范围是b≥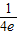 .(14分)
.(14分)点评:本题考查切线方程的求法,考查函数单调性的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答.

练习册系列答案
相关题目