题目内容
如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=1,AD=CD,把△DAC沿对角线AC折起后如图2所示(点D记为点P),点P在平面ABC上的正投影E落在线段AB上,连接PB.
(1)求直线PC与平面PAB所成的角的大小;
(2)求二面角P﹣AC﹣B的大小的余弦值.
(1)求直线PC与平面PAB所成的角的大小;
(2)求二面角P﹣AC﹣B的大小的余弦值.

(1)解:在图1中,∵∠ABC=∠DAB=90°,∠CAB=30°,BC=1,
∴ ,
, ,∠DAC=60°
,∠DAC=60°
∵AD=CD,
∴△DAC为等边三角形.
∴AD=CD=AC=2.
在图2中, ∵点E为点P在平面ABC上的正投影, ∴PE⊥平面ABC.
∵BC 平面ABC, ∴PE⊥BC.
平面ABC, ∴PE⊥BC.
∵∠CBA=90°, ∴BC⊥AB.
∵PE∩AB=E,PE 平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB,
∴BC⊥平面PAB.
∴∠CPB为直线PC与平面PAB所成的角.
在Rt△CBP中,BC=1,PC=DC=2,
∴ . ∵0°<∠CPB<90°, ∴∠CPB=30°.
. ∵0°<∠CPB<90°, ∴∠CPB=30°.
∴直线PC与平面PAB所成的角为30°.
(2)解:取AC的中点F,连接PF,EF.
∵PA=PC, ∴PF⊥AC.
∵PE⊥平面ABC,AC 平面ABC,
平面ABC,
∴PE⊥AC.
∵PF∩PE=P,PF 平面PEF,PE
平面PEF,PE 平面PEF,
平面PEF,
∴AC⊥平面PEF.
∵EF 平面PEF,
平面PEF,
∴EF⊥AC.
∴∠PFE为二面角P﹣AC﹣B的平面角.
在Rt△EFA中, ,
,
∴EF=AFtan30°= ,
, .
.
在Rt△PFA中, .
.
在Rt△PEF中, .
.
∴二面角P﹣AC﹣B的大小的余弦值为 .
.


图1 图2
∴
 ,
, ,∠DAC=60°
,∠DAC=60°∵AD=CD,
∴△DAC为等边三角形.
∴AD=CD=AC=2.
在图2中, ∵点E为点P在平面ABC上的正投影, ∴PE⊥平面ABC.
∵BC
 平面ABC, ∴PE⊥BC.
平面ABC, ∴PE⊥BC.∵∠CBA=90°, ∴BC⊥AB.
∵PE∩AB=E,PE
 平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB, ∴BC⊥平面PAB.
∴∠CPB为直线PC与平面PAB所成的角.
在Rt△CBP中,BC=1,PC=DC=2,
∴
 . ∵0°<∠CPB<90°, ∴∠CPB=30°.
. ∵0°<∠CPB<90°, ∴∠CPB=30°.∴直线PC与平面PAB所成的角为30°.
(2)解:取AC的中点F,连接PF,EF.
∵PA=PC, ∴PF⊥AC.
∵PE⊥平面ABC,AC
 平面ABC,
平面ABC, ∴PE⊥AC.
∵PF∩PE=P,PF
 平面PEF,PE
平面PEF,PE 平面PEF,
平面PEF,∴AC⊥平面PEF.
∵EF
 平面PEF,
平面PEF, ∴EF⊥AC.
∴∠PFE为二面角P﹣AC﹣B的平面角.
在Rt△EFA中,
 ,
,∴EF=AFtan30°=
 ,
, .
.在Rt△PFA中,
 .
.在Rt△PEF中,
 .
.∴二面角P﹣AC﹣B的大小的余弦值为
 .
.

图1 图2

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.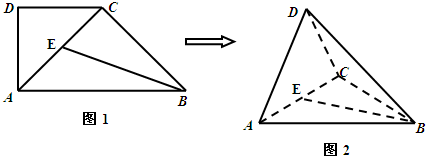 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;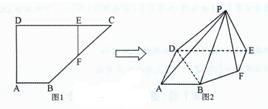 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.