题目内容
在Rt△ABC中,∠C=90°,以斜边AB所在直线为轴将△ABC旋转一周生成两个圆锥,设这两个圆锥的侧面积之积为S1,△ABC的内切圆面积为S2,记 =x.
=x.
(1)求函数f(x)=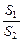 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域.
(2)求函数f(x)的最小值.
 =x.
=x. (1)求函数f(x)=
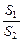 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域. (2)求函数f(x)的最小值.
(1)如图所示:设BC=a,CA=b,AB=c,则斜边AB上的高h= ,
,
∴S1=πah+πbh=

∴f(x)= ①
①
又
代入①消c,得f(x)= .
.
在Rt△ABC中,有a=csinA,b=ccosA(0<A<
 ,则
,则
x= =sinA+cosA=
=sinA+cosA= sin(A+
sin(A+ ). ∴1<x≤
). ∴1<x≤ .
.
(2)f(x)= +6,
+6,
设t=x-1,则t∈(0, -1),y=2(t+
-1),y=2(t+ )+6
)+6
在(0, -1
-1 上是减函数,
上是减函数,
∴当x=( -1)+1=
-1)+1= 时,f(x)的最小值为6
时,f(x)的最小值为6 +8.
+8.
 ,
,∴S1=πah+πbh=


∴f(x)=
 ①
①又

代入①消c,得f(x)=
 .
.在Rt△ABC中,有a=csinA,b=ccosA(0<A<

 ,则
,则x=
 =sinA+cosA=
=sinA+cosA= sin(A+
sin(A+ ). ∴1<x≤
). ∴1<x≤ .
.(2)f(x)=
 +6,
+6,设t=x-1,则t∈(0,
 -1),y=2(t+
-1),y=2(t+ )+6
)+6在(0,
 -1
-1 上是减函数,
上是减函数,∴当x=(
 -1)+1=
-1)+1= 时,f(x)的最小值为6
时,f(x)的最小值为6 +8.
+8.
练习册系列答案
相关题目
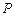 与日产量
与日产量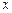 的函数关系是
的函数关系是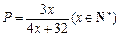 .
.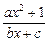 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.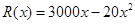 (单位:元),其成本函数为
(单位:元),其成本函数为 (单位:元),利润是收入与成本之差。
(单位:元),利润是收入与成本之差。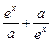 是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数.
是R上的偶函数,(1)求a的值;(2)证明: f(x)在(0,+∞)上是增函数. 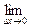
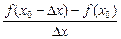 的值是
的值是 在点
在点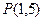 和
和 处的切线方程。
处的切线方程。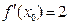 ,则
,则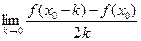 等于( )
等于( )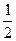
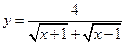 的导数.
的导数.