题目内容

已知两组数据x1，x2，…，xn与y1，y2，…，yn，它们的平均数分别是
.
x
和
.
y
，则新的一组数据2x1-3y1+1，2x2-3y2+1，…，2xn-3yn+1的平均数是（　　）
A．2
.
x
-3
.
y
B．2
.
x
-3
.
y
+1		C．4
.
x
-9
.
y
D．4
.
x
-9
.
y
+1
由已知，（x1+x2+…+xn）=n
.
x
，
（y1+y2+…+yn）=n
.
y
，
新的一组数据2x1-3y1+1，2x2-3y2+1，…，2xn-3yn+1的平均数为
（2x1-3y1+1+2x2-3y2+1+…+2xn-3yn+1）÷n
=[2（x1+x2+…+xn）-3（y1+y2+…+yn）+n]÷n
=2
.
x
-3
.
y
+1
故选B
练习册系列答案
相关题目
已知两组数据x1，x2，…，xn与y1，y2，…，yn，它们的平均数分别是
.
x
和
.
y
，则新的一组数据2x1-3y1+1，2x2-3y2+1，…，2xn-3yn+1的平均数是
 
．在总体中抽取了一个样本，为了便于统计，将样本中的每个数据乘以100后进行分析，得出新样本平均数为3，则估计总体的平均数为
 
．
某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．
（I）已知两组技工在单位时间内加工的合格零件数的平均数都为10，分别求出m，n的值；
（Ⅱ）分别求出甲、乙两组技工在单位时间内加工的合格零件数的方差
S
2
甲
和
S
2
乙
，并由此分析两组技工的加工水平；
（Ⅲ）质检部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，若两人加工的合格零件数之和大于17，则称该车间“待整改”，求该车间“待整改”的概率．（注：方差，s2=
1
n
[(x1-
.
x
)2+(x2-
.
x
)2+…+(xn-
.
x
)2，其中
.
x
为数据x1，x2，…，xn的平均数）
（2007•肇庆二模）已知两组数据x1，x2，…，xn与y1，y2，…，yn，它们的平均数分别是
.
x
和
.
y
，则新的一组数据2x1-3y1+1，2x2-3y2+1，…，2xn-3yn+1的平均数是（　　）
某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．
（I）已知两组技工在单位时间内加工的合格零件数的平均数都为10，分别求出m，n的值；
（Ⅱ）分别求出甲、乙两组技工在单位时间内加工的合格零件数的方差
S2甲
和
S2乙
，并由此分析两组技工的加工水平；
（Ⅲ）质检部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，若两人加工的合格零件数之和大于17，则称该车间“待整改”，求该车间“待整改”的概率．（注：方差，s2=
1
n
[(x1-
.
x
)2+(x2-
.
x
)2+…+(xn-
.
x
)2，其中
.
x
为数据x1，x2，…，xn的平均数）
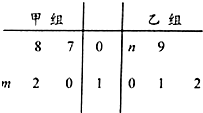
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网