题目内容
10.为了解高一年级1200名学生的视力情况,采用系统抽样的方法,从中抽取容量为60的样本,则分段间隔为( )| A. | 10 | B. | 20 | C. | 40 | D. | 60 |
分析 利用系统抽样定义直接求解.
解答 解:为了解高一年级1200名学生的视力情况,
采用系统抽样的方法,从中抽取容量为60的样本,
则分段间隔为:$\frac{1200}{60}$=20.
故选:B.
点评 本题考查抽样分段间隔的求法,是基础题,解题是要认真审题,注意系统抽样定义的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.设p是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{9}$=1上一点,双曲线的一条渐近线方程为3x-2y=0,F1,F2分别是双曲线的左、右焦点,若|PF1|=5,则|PF2|=( )
| A. | 1或5 | B. | 1或9 | C. | 1 | D. | 9 |
5.设α,β是两个不同的平面,m,n,l 是三条不同的直线,下列命题中正确的是( )
| A. | 若α∩β=l,m?α,n?β,则m,n一定相交 | B. | 若α∥β,m?α,n?β,则m,n一定平行 | ||
| C. | 若α∥β,m∥α,n∥β,则m,n一定平行 | D. | 若α⊥β,m⊥α,n⊥β,则m,n一定垂直 |
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右焦点为F,右顶点为A,一条渐近线方程为y=2$\sqrt{2}$x,且|AF|=2,则该双曲线的实轴长为( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
19.若等比数列{an}的前n项和Sn=3n-1,则其公比为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
20.已知m、n为两条不同的直线,α、β、γ为三个不同的平面,下列结论正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若α∥γ,β∥γ,则α∥β | ||
| C. | 若α⊥β,m∥α,则m⊥β | D. | 若α⊥β,m?α,n?β,则m⊥n |
 某校高一年级某次数学竞赛随机抽取100名学生的成绩,分组为[50,60),[60,70),[70,80),[80,90),[90,100],统计后得到频率分布直方图如图所示:
某校高一年级某次数学竞赛随机抽取100名学生的成绩,分组为[50,60),[60,70),[70,80),[80,90),[90,100],统计后得到频率分布直方图如图所示: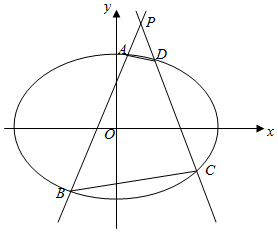 如图,在平面直角坐标系xOy中,已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1.
如图,在平面直角坐标系xOy中,已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1.