题目内容
11.已知集合M={x|y=lg$\frac{1-x}{x}$},N={y|y=x2+2x+3},则(∁RM)∩N=( )| A. | (0,1) | B. | [1,+∞) | C. | [2,+∞) | D. | (-∞,0]∪[1,+∞) |
分析 化简集合M、N,利用集合的基本运算即求出结论.
解答 解:M={x丨y=lg$\frac{1-x}{x}$}={x丨$\frac{1-x}{x}$>0}={x|0<x<1}=(0,1),
N={y|y=x2+2x+3}={y|y=(x+1)2+2≥2}=[2,+∞),
∴∁RM=(-∞,0]∪[1,+∞),
∴(∁RM)∩N=[2,+∞).
故选:C.
点评 本题主要考查了集合的基本运算问题,利用函数的性质求出相应的集合是解题的关键,是基础题.

练习册系列答案
相关题目
1.在数列{an}中,a1=1,$\frac{{a}_{n+1}}{{a}_{n}}$=3n,则an为( )
| A. | an=3n | B. | an=3${\;}^{\frac{n(n+1)}{2}}$ | C. | an=3${\;}^{\frac{n(n-1)}{2}}$ | D. | an=3${\;}^{\frac{n}{2}}$ |
3.已知变量x,y之间的线性回归方程为$\widehat{y}$=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )
| x | 6 | 8 | 10 | 12 |
| y | 6 | m | 3 | 2 |
| A. | 变量x,y之间呈现负相关关系 | |
| B. | m=4 | |
| C. | 可以预测,当x=11时,y=2.6 | |
| D. | 由表格数据知,该回归直线必过点(9,4) |
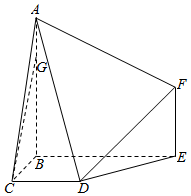 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.