题目内容
定义在R上的奇函数f(x)有最小正周期4,且x∈(0,2)时,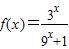 .
.(1)求f(x)在[-2,2]上的解析式;
(2)判断f(x)在(0,2)上的单调性,并给予证明;
(3)当λ为何值时,关于方程f(x)=λ在[-2,2]上有实数解?
【答案】分析:(1)可设x∈(-2,0),则-x∈(0,2)由x∈(0,2)时,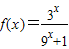 =
=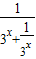 可求f(-x),再由奇函数的性质可求
可求f(-x),再由奇函数的性质可求
(2)利用函数的单调性的定义进行证明即可
(3)转化为求解函数f(x)在(-2,2)上的值域,结合(2)可先求f(x)在(0,2)上的值域,然后结合奇函数的对称性可求在(-2,0)上的值域
解答:解:(1)设x∈(-2,0),则-x∈(0,2)
∵x∈(0,2)时,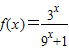 =
=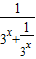
∴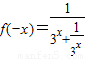
由函数f(x)为奇函数可得,f(-x)=-f(x)
∴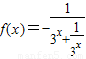
∵f(0)=0,
∵周期为4且为奇函数,f(-2)=-f(2)=f(2)
∴f(-2)=f(2)=0
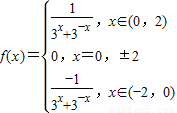
(2)设0<x1<x2<2
令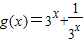
则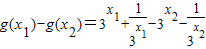 =
=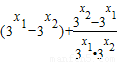
=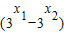
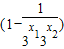
∵0<x1<x2<2
∴g(x1)<g(x2)
∴函数g(x)在(0,2)单调递增,且g(x)>0
∴f(x)在(0,2)单调递减
(3)由(2)可得当0<x<2时,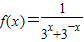 单调递减
单调递减
故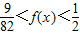
由奇函数的对称性可得,x∈(-2,0)时,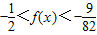
当x=0时,f(0)=0
∵关于方程f(x)=λ在[-2,2]上有实数解
∴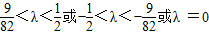
点评:本题主要考查了利用函数的奇函数的 性质求解函数的解析式,及利用函数单调性的定义进行判断函数单调性的问题,还考查了方程与函数的相互转化的思想在解题中的应用,属于综合试题
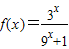 =
=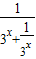 可求f(-x),再由奇函数的性质可求
可求f(-x),再由奇函数的性质可求(2)利用函数的单调性的定义进行证明即可
(3)转化为求解函数f(x)在(-2,2)上的值域,结合(2)可先求f(x)在(0,2)上的值域,然后结合奇函数的对称性可求在(-2,0)上的值域
解答:解:(1)设x∈(-2,0),则-x∈(0,2)
∵x∈(0,2)时,
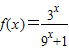 =
=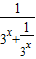
∴
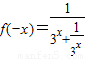
由函数f(x)为奇函数可得,f(-x)=-f(x)
∴
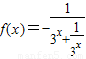
∵f(0)=0,
∵周期为4且为奇函数,f(-2)=-f(2)=f(2)
∴f(-2)=f(2)=0
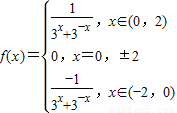
(2)设0<x1<x2<2
令
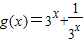
则
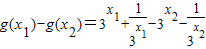 =
=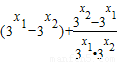
=
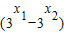
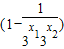
∵0<x1<x2<2
∴g(x1)<g(x2)
∴函数g(x)在(0,2)单调递增,且g(x)>0
∴f(x)在(0,2)单调递减
(3)由(2)可得当0<x<2时,
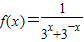 单调递减
单调递减故
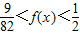
由奇函数的对称性可得,x∈(-2,0)时,
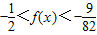
当x=0时,f(0)=0
∵关于方程f(x)=λ在[-2,2]上有实数解
∴
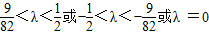
点评:本题主要考查了利用函数的奇函数的 性质求解函数的解析式,及利用函数单调性的定义进行判断函数单调性的问题,还考查了方程与函数的相互转化的思想在解题中的应用,属于综合试题

练习册系列答案
相关题目
定义在R上的奇函数f(x)满足f(2x)=-2f(x),f(-1)=
,则f(2)的值为( )
| 1 |
| 2 |
| A、-1 | B、-2 | C、2 | D、1 |