题目内容
已知函数
．（1）求a的值；
（2）判断函数f（x）的奇偶性（须有证明过程）；
（3）求f（x）在区间（0，+∞）的单调性（须有证明过程）．
【答案】分析：（1）由函数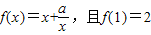
，可得 1+a=2，解得 a 的值．
（2）函数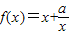
的定义域为{x|x≠1}，关于原点对称，且f（-x）=-f（x），可得函数是奇函数．
（3）设 0＜x1＜x2＜1，化简f（x1 ）-f（x2）的解析式，可得f（x1 ）-f（x2）＞0，故f（x）在（0，1）上是减函数，同理可证f（x）在（1，+∞）上是增函数．
解答：解：（1）∵函数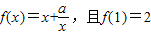
，∴1+a=2，解得 a=1．
（2）函数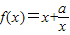
的定义域为{x|x≠1}，关于原点对称，
且f（-x）=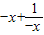
=-（
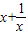）=-f（x），故函数是奇函数．
（3）设 0＜x1＜x2＜1，由于
f（x1 ）-f（x2）=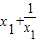
-（
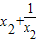）=（x1-x2）+（
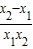）=（x1-x2） （1-
），
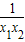由 0＜x1＜x2＜1可得 x1-x2＜0，（1-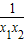
）＜0，故有f（x1 ）-f（x2）＞0，
故f（x）在（0，1）上是减函数，
同理可得f（x）在（1，+∞）上是增函数．
点评：本题主要考查函数的奇偶性和单调性的判断和证明，求函数的值，属于中档题．
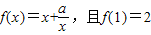，可得 1+a=2，解得 a 的值．（2）函数
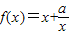的定义域为{x|x≠1}，关于原点对称，且f（-x）=-f（x），可得函数是奇函数．（3）设 0＜x1＜x2＜1，化简f（x1 ）-f（x2）的解析式，可得f（x1 ）-f（x2）＞0，故f（x）在（0，1）上是减函数，同理可证f（x）在（1，+∞）上是增函数．
解答：解：（1）∵函数
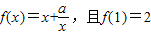，∴1+a=2，解得 a=1．（2）函数
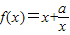的定义域为{x|x≠1}，关于原点对称，且f（-x）=
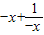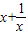=-（）=-f（x），故函数是奇函数．（3）设 0＜x1＜x2＜1，由于
f（x1 ）-f（x2）=
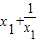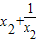-（）=（x1-x2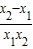）+（）=（x1-x2） （1-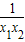），由 0＜x1＜x2＜1可得 x1-x2＜0，（1-
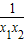）＜0，故有f（x1 ）-f（x2）＞0，故f（x）在（0，1）上是减函数，
同理可得f（x）在（1，+∞）上是增函数．
点评：本题主要考查函数的奇偶性和单调性的判断和证明，求函数的值，属于中档题．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
．
，
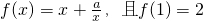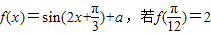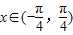时，求f（x）的取值范围．
，
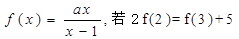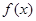在区间 
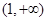的单调性.
．