题目内容
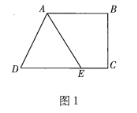
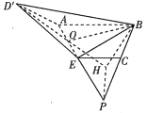
【题目】如图1,在梯形![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,将
,将![]() 沿
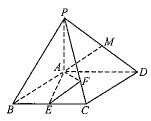
沿![]() 翻折,使翻折后的二面角
翻折,使翻折后的二面角![]() 的余弦值为
的余弦值为![]() ,如图2.
,如图2.
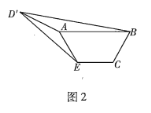
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)先根据菱形的性质证得线线垂直,再根据线面垂直的判定定理证得线面垂直,最后根据线面垂直的性质定理证得线线垂直;
(2)先通过作辅助线找到所求的线面角及二面角![]() 的平面角,再通过解三角形求相关线段的长度,即可得线面角的正弦值,也可根据垂直关系建立空间直角坐标系进行求解.
的平面角,再通过解三角形求相关线段的长度,即可得线面角的正弦值,也可根据垂直关系建立空间直角坐标系进行求解.
解:(1)在梯形![]() 中,
中,
连接![]() ,
,
记![]() .
.
由题意易得![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,
所以四边形![]() 是菱形,
是菱形,
所以![]() ,
,
所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() .
.
(2)因为![]() 平面
平面![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
如图所示,
因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
延长![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
由![]() ,
,
得二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
所以![]() .
.
由四边形![]() 是菱形,
是菱形,
且易得![]() ,
,
得![]() 为等边三角形,
为等边三角形,
所以![]() ,
,
所以![]() .
.
在![]() 中,易知
中,易知![]() 为
为![]() 的中位线,
的中位线,![]() ,
,
所以![]() ,
,
所以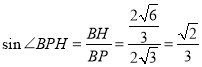 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后25组同学得分如下表:
组别号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
男同学得分 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 4 | 4 | 5 | 5 | 4 |
女同学得分 | 4 | 3 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 3 | 5 |
分差 | 1 | 1 | 1 | 0 | -1 | 0 | 1 | -1 | -1 | -1 | 0 | 2 | -1 |
组别号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
男同学得分 | 4 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | 3 | 3 | |
女同学得分 | 5 | 3 | 4 | 5 | 4 | 3 | 5 | 5 | 3 | 4 | 5 | 5 | |
分差 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 2 | 0 | -2 | -2 | |
(I)完成![]() 列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
(Ⅱ)某课题研究小组假设各组男女同学分差服从正态分布![]() ,首先根据前20组男女同学的分差确定
,首先根据前20组男女同学的分差确定![]() 和
和![]() ,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与
,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与![]() 的差的绝对值分别为
的差的绝对值分别为![]() ,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在
,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在![]() ;②记满足
;②记满足![]() 的i的个数为k,在服从正态分布
的i的个数为k,在服从正态分布![]() 的总体(个体数无穷大)中任意取5个个体,其中落在区间
的总体(个体数无穷大)中任意取5个个体,其中落在区间![]() 内的个体数大于或等于k的概率为P,
内的个体数大于或等于k的概率为P,![]() .
.
试问该课题研究小组是否会接受该模型.
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
参考公式和数据: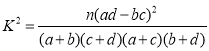
![]() ,
,![]() ;若
;若![]() ,有
,有![]() ,
,![]() .
.