题目内容
19．已知△ABC的两内角A、B适合方程8sin2x+3sin2x-4=0，并且A＜B，求这三角形三边之比．分析 利用二倍角公式化简条件式得到cos2x，利用2倍角公式计算sinx，即sinA．sinB的值，则sinC=sin（A+B），利用正弦定理得出三边之比等于sinA：sinB：sinC．
解答 解：∵8sin2x+3sin2x-4=0，∴4-4cos2x+3sin2x-4=0，即3sin2x-4cos2x=0．
∴tan2x=$\frac{4}{3}$．
∴cos2x=±$\frac{3}{5}$．
∵cos2x=1-2sin2x=$±\frac{3}{5}$，
∴sinx=±$\frac{\sqrt{5}}{5}$或sinx=±$\frac{2\sqrt{5}}{5}$．
∴0＜A＜B＜π，
∴sinA=$\frac{\sqrt{5}}{5}$，sinB=$\frac{2\sqrt{5}}{5}$．
∴cosA=$\frac{2\sqrt{5}}{5}$，cosB=$±\frac{\sqrt{5}}{5}$．
∴sinC=sin（A+B）=1或$\frac{3}{5}$．
∴a；b：c=sinA；sinB：sinC=1；2：$\sqrt{5}$或5：10：3$\sqrt{5}$．
点评 本题考查了三角函数的恒等变换，正弦定理得应用，属于中档题．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
相关题目
9．定义在R上的函数f（x）满足$f（{x+2}）=\frac{1}{2}f（x）$，当x∈[0，2）时，$f（x）=\left\{\begin{array}{l}\frac{1}{2}-2{x^2}，0≤x＜1\\-{2^{1-|{x-\frac{3}{2}}|}}，1≤x＜2\end{array}\right.$，函数g（x）=x3+3x2+m．若?s∈[-4，-2），?t∈[-4，-2），不等式f（s）-g（t）≥0成立，则实数m的取值范围是（ ）
| A． | （-∞，-12] | B． | （-∞，-4] | C． | （-∞，8] | D． | $（{-∞，\frac{31}{2}}]$ |
11．在△ABC中，角A、B、C的对边分别为a、b、c，若cos2A+cos2C+$\sqrt{2}$sinAsinC=1+cos2B．则$\sqrt{2}$sinA+cosC的最大值是（ ）
| A． | 1 | B． | 2 | C． | $\frac{3\sqrt{2}}{2}$ | D． | $\sqrt{5}$ |
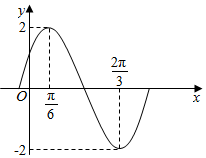函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）（x∈R）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式并求函数f（x）的单调递增区间；