题目内容

已知f（x+2）=x²+2x-3，函f（x）的表达式是

x²-2x-3

x²-2x-3

．

分析：令t=x+2换元，将x=t-2代入f（x+2）=x²+2x-3即可．

解答：解：令t=x+2，则x=t-2代入f（x+2）=x²+2x-3得：
f（t）=（t-2）²+2（t-2）-3
=t²-2t-3．
∴f（x）=x²-2x-3．
故答案为：x²-2x-3．

点评：本题考查换元法求函数解析式，考查转化与运算能力，属于基础题．

练习册系列答案

实验班中考总复习系列答案

亮点激活期末冲刺大试卷系列答案

全优学习达标训练系列答案

毕业会考阶梯模拟卷系列答案

小学升学多伦夯基总复习系列答案

同步练习目标与测试系列答案

复习计划风向标暑系列答案

开心快乐假期作业暑假作业西安出版社系列答案

学业考试综合练习册系列答案

名题训练系列答案

相关题目

5、已知f（x+1）=x²-x-2，则f（x）的解析式是（　　）

A、f（x）=x²+x-3

B、f（x）=x²+x+1

C、f（x）=x²-3x

D、f（x）=x²-3x-2

已知f 1(x)=|3x-1|，f2(x)=|a•3x-9|(a＞0)，x∈R，且f（x）=

f1(x)，f1(x)≤f2(x)

f2(x)，f1(x)＞f2(x)

（1）当a=1时，求f（x）的解析式；
（2）在（1）的条件下，若方程f（x）-m=0有4个不等的实根，求实数m的范围；
（3）当2≤a＜9时，设f（x）=f₂（x）所对应的自变量取值区间的长度为l（闭区间[m，n]的长度定义为n-m），试求l的最大值．

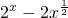已知f（x）是R上的偶函数，当x≥0时，f （x）= $数学公式$ ，又a是函数g （x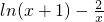）= $数学公式$ 的正零点，则f（-2），f（a），f（1.5）的大上关系是

A.
f（1.5）＜f（a）＜f（-2）
B.
f（-2）＜f（1.5）＜f（a）
C.
f（a）＜f（1.5）＜f（-2）
D.
f（1.5）＜f（-2）＜f（a）

已知f（x）是R上的增函数，点A（-2，1）、B（2，3）在它的图象上，那么，不等式|f^-1（x）|＜2的解集是（）
A．{x|-1＜x＜1}
B．{x|-2＜x＜2}
C．{x|-2＜x＜3}
D．{x|1＜x＜3}

已知f（x）是R上的增函数，点A（-2，1）、B（2，3）在它的图象上，那么，不等式|f^-1（x）|＜2的解集是（）
A．{x|-1＜x＜1}
B．{x|-2＜x＜2}
C．{x|-2＜x＜3}
D．{x|1＜x＜3}