题目内容
f（x）=x2，g（x）=2x，h（x）=log2x，当x∈（4，+∞）时，三个函数增长速度比较，其大小关系是________．
g（x）＞f（x）＞h（x）
分析：先对三个函数分别求导，然后根据x的范围判断导函数的大小关系，进而可判断其对应函数的增长速度的快慢．
解答：∵f（x）=x2，g（x）=2x，h（x）=log2x
∴f'（x）=2x，g'（x）=2xln2，h'（x）=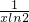
当x＞4时，2xln2＞2x＞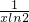
∴g'（x）＞f'（x）＞h'（x）
故三个函数的增长速度为g（x）＞f（x）＞h（x）
故答案为：g（x）＞f（x）＞h（x）
点评：本题主要考查求导运算和导数的几何意义．考查对基础知识的灵活运用．
分析：先对三个函数分别求导，然后根据x的范围判断导函数的大小关系，进而可判断其对应函数的增长速度的快慢．
解答：∵f（x）=x2，g（x）=2x，h（x）=log2x
∴f'（x）=2x，g'（x）=2xln2，h'（x）=
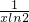
当x＞4时，2xln2＞2x＞
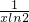
∴g'（x）＞f'（x）＞h'（x）
故三个函数的增长速度为g（x）＞f（x）＞h（x）
故答案为：g（x）＞f（x）＞h（x）
点评：本题主要考查求导运算和导数的几何意义．考查对基础知识的灵活运用．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目