题目内容
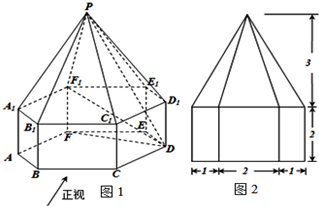 (2011•佛山二模)如图1,已知几何体的下部是一个底面为正六边形、侧面全为矩形的棱柱,上部是一个侧面全为等腰三角形的棱锥,图2是该几何体的主视图.
(2011•佛山二模)如图1,已知几何体的下部是一个底面为正六边形、侧面全为矩形的棱柱,上部是一个侧面全为等腰三角形的棱锥,图2是该几何体的主视图.(1)求该几何体的体积;
(2)证明:DF1平面PA1F1.
分析:(1)由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,分别求体积,即可得出结论;
(2)证明A1F1⊥平面DFF1,可得A1F1⊥DF1;利用勾股定理,可得DF1⊥PF1,利用线面垂直的判定定理,可得结论.
(2)证明A1F1⊥平面DFF1,可得A1F1⊥DF1;利用勾股定理,可得DF1⊥PF1,利用线面垂直的判定定理,可得结论.
解答: (1)解:由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,
(1)解:由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,
∴正六棱柱的体积为:V1=Sh=6×
×2×
×2=12
; …(3分)
正六棱锥的体积为:V2=
Sh=
×6×
×2×
×3=6
; …(6分)
∴该几何体的体积的体积为V=V1+V2=18
. …(7分)
(2)证明:∵侧面全为矩形,∴AF⊥FF1;
在正六边形ABCDEF中,AF⊥DF,…(8分)
∵DF∩FF1=F,∴AF⊥平面DFF1; …(9分)
∵AF∥A1F1,∴A1F1⊥平面DFF1;
又DF1?平面DFF1,∴A1F1⊥DF1;…(11分)
(注:也可以由勾股定理得到)
在△DFF1中,FF1=2,DF=2
,∴DF1=4,
∵PF1=PD1=
;
∴在平面PA1ADD1中,如图所示,PD=
=
,
∴DF12+PF12=PD2,故DF1⊥PF1;…(13分)
∵A1F1∩PF1=F1,∴DF1⊥平面PA1F1. …(14分)
 (1)解:由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,
(1)解:由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,∴正六棱柱的体积为:V1=Sh=6×
| 1 |
| 2 |
| 3 |
| 3 |
正六棱锥的体积为:V2=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∴该几何体的体积的体积为V=V1+V2=18
| 3 |
(2)证明:∵侧面全为矩形,∴AF⊥FF1;
在正六边形ABCDEF中,AF⊥DF,…(8分)
∵DF∩FF1=F,∴AF⊥平面DFF1; …(9分)
∵AF∥A1F1,∴A1F1⊥平面DFF1;
又DF1?平面DFF1,∴A1F1⊥DF1;…(11分)
(注:也可以由勾股定理得到)
在△DFF1中,FF1=2,DF=2
| 3 |
∵PF1=PD1=
| 13 |
∴在平面PA1ADD1中,如图所示,PD=
| 52+22 |
| 29 |
∴DF12+PF12=PD2,故DF1⊥PF1;…(13分)
∵A1F1∩PF1=F1,∴DF1⊥平面PA1F1. …(14分)
点评:本题考查几何体体积的计算,考查线面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 (2011•佛山二模)如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+B.则中午12点时最接近的温度为( )
(2011•佛山二模)如图,某地一天从6~14时的温度变化曲线近似满足函数:y=Asin(ωx+φ)+B.则中午12点时最接近的温度为( )