Question

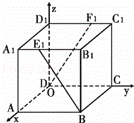
如图，在空间直角坐标系xoy中，正方体ABCD﹣A₁B₁C₁D₁的棱长为1，E₁在A₁B₁上，F₁在C₁D₁上，且B₁E₁=D₁F₁=．

（Ⅰ）求向量，的坐标；

（Ⅱ）求BE₁与DF₁所成的角的余弦值．

Answer 1

考点：

异面直线及其所成的角；空间向量运算的坐标表示．

专题：

计算题．

分析：

（Ⅰ）由题意可得点得B，E₁，D，F₁的坐标，由向量的坐标运算可得，的坐标；

（Ⅱ）由（Ⅰ）所得的，与的坐标，由夹角公式可得这两个向量夹角的余弦值，进而可得所求．

解答：

解：（Ⅰ）由题意可得B（1，1，0），E₁（1，，1），D（0，0，0），F₁（0，，

故，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）

（Ⅱ）由（Ⅰ）可知，，

∴，，

，

所以，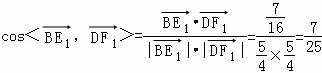

故BE₁与DF₁所成的角的余弦值为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）

点评：

本题考查异面直线所成的角，涉及向量的坐标运算，属中档题．