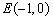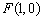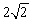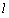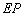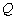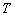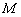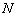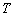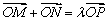题目内容
在平面直角坐标系中已知A(-1,2),B(2,-1),现沿x轴将坐标平面折成60°的二面角,则折叠后A、B两点间的距离为
2
| 3 |
2
.| 3 |
分析:平面直角坐标系中已知A(-1,2),B(2,-1),现沿x轴将坐标平面折成60°的二面角后,点A在原平面直角坐标系中的射影为C(-1,-1),则AC=
=
,BC=3,由此能求出AB.
| 22-12 |
| 3 |
解答:解:平面直角坐标系中已知A(-1,2),B(2,-1),
沿x轴将坐标平面折成60°的二面角后,
A点的对应点是A‘,A’在平面xOy上的射影是C,作CD⊥x轴,交x轴于D点,
在△ACD中,由题设知AD=2,DC⊥面ABC,DC=1,C(-1,-1)
∴AC=
=
,BC=3,
∵AC⊥BC,
∴AB=
=
=2
.
故答案为:2
.


沿x轴将坐标平面折成60°的二面角后,
A点的对应点是A‘,A’在平面xOy上的射影是C,作CD⊥x轴,交x轴于D点,
在△ACD中,由题设知AD=2,DC⊥面ABC,DC=1,C(-1,-1)
∴AC=
| 22-12 |
| 3 |
∵AC⊥BC,
∴AB=
| AC2+BC2 |
| 3+9 |
| 3 |
故答案为:2
| 3 |


点评:本题考查与二面角有关的立体几何综合题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 在平面直角坐标系中已知点A(3,0),P是圆x2+y2=1上一个动点,且∠AOP的平分线交PA于Q点,求Q点的轨迹的极坐标方程.
在平面直角坐标系中已知点A(3,0),P是圆x2+y2=1上一个动点,且∠AOP的平分线交PA于Q点,求Q点的轨迹的极坐标方程. 中,已知直线
中,已知直线 被圆[
被圆[ 截得的弦长为
截得的弦长为
 的方程
的方程 轴相交于
轴相交于 ,
, 两点,点
两点,点 为圆
为圆 ,
, 交
交 轴于
轴于 ,
, 两点.当点
两点.当点 为直径的圆
为直径的圆 是否经过圆
是否经过圆