题目内容
已知平面上四点A,B,C满足(
+
)•
=0,则△ABC的形状是( )
| BC |
| BA |
| AC |
分析:取AC的中点D,连接BD,利用向量的和的几何意义可判断△ABC的形状
解答:解:取AC的中点D,连接BD,
则2
=
+
,
∵(
+
)•
=0,
∴2
•
=0,
∴|AB|=|BC|,
∴△ABC为等腰三角形.
故选A.
则2
| BD |
| BC |
| BA |
∵(
| BC |
| BA |
| AC |
∴2
| BD |
| AC |
∴|AB|=|BC|,
∴△ABC为等腰三角形.
故选A.
点评:本题考查三角形的形状判断,考查平面向量数量积的运算,理解向量的和的几何意义是关键,属于中档题.

练习册系列答案
相关题目
 ,则△ABC的形状是
,则△ABC的形状是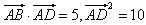 ,
,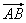 及
及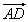 表示
表示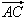 。
。 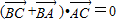 ,则△ABC的形状是( )
,则△ABC的形状是( )