题目内容
5.数列{an}满足a1=1,an=$\frac{n{a}_{n-1}}{{a}_{n-1}+2n-2}$(n≥2,n∈N*).(1)求a2,a3,a4的值;
(2)求数列{an}的通项公式;
(3)设bn=(1-$\frac{1}{{2}^{n}}$)an,求数列{bn}的前n项和.
分析 (1)由a1=1,an=$\frac{n{a}_{n-1}}{{a}_{n-1}+2n-2}$(n≥2,n∈N*),分别取n=2,3,4即可得出.可得a2,a3,a4.
(2)由an=$\frac{n{a}_{n-1}}{{a}_{n-1}+2n-2}$,两边取倒数化简可得:$\frac{n}{{a}_{n}}$+1=2($\frac{n-1}{{a}_{n-1}}$+1),利用等比数列的通项公式即可得出.
(3)bn=(1-$\frac{1}{{2}^{n}}$)an=$\frac{n}{{2}^{n}}$.利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)由a1=1,an=$\frac{n{a}_{n-1}}{{a}_{n-1}+2n-2}$(n≥2,n∈N*).可得a2=$\frac{2{a}_{1}}{{a}_{1}+2×2-2}$=$\frac{2}{3}$,同理可得a3=$\frac{3}{7}$,a4=$\frac{4}{15}$.
(2)由an=$\frac{n{a}_{n-1}}{{a}_{n-1}+2n-2}$,两边取倒数化简可得:$\frac{n}{{a}_{n}}$+1=2($\frac{n-1}{{a}_{n-1}}$+1),
∴数列$\{\frac{n}{{a}_{n}}+1\}$是等比数列,首项为2,公比为2.
∴$\frac{n}{{a}_{n}}$+1=2n,
解得an=$\frac{n}{{2}^{n}-1}$.
(3)bn=(1-$\frac{1}{{2}^{n}}$)an=$\frac{n}{{2}^{n}}$.
∴数列{bn}的前n项和Sn=$\frac{1}{2}+\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$.
$\frac{1}{2}{S}_{n}$=$\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n}}$+$\frac{n}{{2}^{n+1}}$,
∴$\frac{1}{2}{S}_{n}$=$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=1-$\frac{2+n}{{2}^{n+1}}$.
∴Sn=$2-\frac{2+n}{{2}^{n}}$.
点评 本题考查了“错位相减法”、等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| A. | [-2,2] | B. | (0,+∞) | C. | (0,2] | D. | [0,2] |
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
| A. | (1,2) | B. | (-1,0) | C. | (-2,-1) | D. | (-6,-1) |
| A. | -2 | B. | 4 | C. | -6 | D. | 6 |
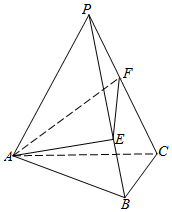 正三棱锥P-ABC的侧面是底边长为a,顶角为30°的等腰三角形.过点A作这个三棱锥的截面AEF,点E、F分别在棱PB、PC上.
正三棱锥P-ABC的侧面是底边长为a,顶角为30°的等腰三角形.过点A作这个三棱锥的截面AEF,点E、F分别在棱PB、PC上.