题目内容
如图所示，正方体ABCD—A1B1C1D1中，点N在BD上，点M在B1C上，且CM=DN.
（1）求证：MN∥平面AA1B1B；
（2）设正方体ABCD—A1B1C1D1的棱长为a.问CM为何值时，MN有最小值？并求出最小值.
解析：要证线面平行，只要在面AA1B1B中找到一条直线与MN平行即可，利用正方体的性质,B1C=BD.由CM=DN得B1M=BN，于是作ME∥BC交BB1于E.作NF∥AD交AB于F，利用比例线段性质证明MN EF.第（2）题利用（1）的结论，MN=EF.设BE=x,由正方形性质得CM=
x,即DN=
x.于是AF=x.在Rt△BEF中，建立了EF的目标函数，利用函数观点求解.?
（1）证明：作ME∥BC交BB1于E，NF∥AD交AB于F，连结EF.∴
和
又由正方体性质得BD=B1C.?
又∵CM=DN ，∴B1M=BN.∴
.∴
.?
又∵BC=AD，∴ME=NF.又AD 
BC,∴ME∥NF.?
∴ME 
NF.∴MEFN是平行四边形.∴MN 
EF.?
又∵EF
面ABB1A1，MN
面ABB1A1，?
∴MN∥面ABB1A1.?
（2）设BE=x,在正方形BB1CC1中，MC=
x.?
又∵DN=CM，∴DN=
x.?
在正方形ABCD中，DN=
x,∴AF=x.∴FB=a -x.?
在Rt△EBF中，EF2=BE2+FB2=x2+(a-x)2=2x2-2ax+a2.?
∴MN=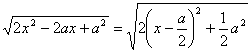
.?
当x=
时，MN的最小值为
.?
因此当x=
时，MN取得最小值
.
练习册系列答案
相关题目
如图所示，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，G为DD1上一点，且D1G：GD=1：2，AC∩BD=O，求证：平面AGO∥平面D1EF．
如图所示，正方体ABCD-A1B1C1D1中，E、F分别是正方体ADD1A1和ABCD的中心，G是C1C的中点，设GF、C1F与AB所成的角分别为α、β，则α+β等于
如图所示，正方体ABCD－A1B1C1D1的棱长为1，点M在AB上，且AM＝
AB，点P在平面ABCD上，且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1，在平面直角坐标系xAy中，动点P的轨迹方程是________．