题目内容
已知数列 中,
中, ,
,
①当b=1时, =12;
=12;
②存在 ,数列
,数列 成等比数列;
成等比数列;
③当 时,数列
时,数列 是递增数列;
是递增数列;
④当 时数列
时数列 是递增数列
是递增数列
以上命题为真命题的是 .(写出所有真命题对应的序号)
①②③
【解析】
试题分析:①由题根据所给条件直接验证即可;②假设存在满足条件的 值,根据等比数列定义分析,然后根据所给条件利用系数相等求得对应的
值,根据等比数列定义分析,然后根据所给条件利用系数相等求得对应的 即可;③④由题根据所给条件应用累加法不难得到数列的单调性,从而判断对应命题的真假;
即可;③④由题根据所给条件应用累加法不难得到数列的单调性,从而判断对应命题的真假;
①当b=1时,易知 ,故①对;
,故①对;
②若 为等比数列,设公比为q,则
为等比数列,设公比为q,则 ,
,
 ,故存在
,故存在 使数列
使数列 为等比数列;故②对;
为等比数列;故②对;
③由题可得 ,
,
 ,所以b>1时,数列
,所以b>1时,数列 为递增数列;故③对;
为递增数列;故③对;
④由题可得
所以
 ,当
,当 时数列
时数列 是递减数列,故④错.
是递减数列,故④错.
考点:等比数列的性质,数列与函数的关系

练习册系列答案
相关题目

 为圆心且与直线
为圆心且与直线 相切的圆的方程为____ __ _____.
相切的圆的方程为____ __ _____.
 B.
B. C.
C. D.
D.
 ,若
,若 为实数),则
为实数),则 的值为( )
的值为( ) D.
D.
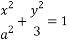 的右焦点为F,直线
的右焦点为F,直线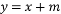 与椭圆E交于A,B两点.若△EAB周长的最大值是8,则m的值等于 ( ).
与椭圆E交于A,B两点.若△EAB周长的最大值是8,则m的值等于 ( ). D. 2
D. 2 则
则 是( ).
是( ). B.
B.
 D.
D.
 “
“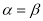 ”是“
”是“ ”的
”的 =( )
=( )  B.
B. C.
C. D.
D.