题目内容
函数f(x)=
(a∈R).
(1)若f(x)在点(1,f(1))处的切线斜率为
,求实数a的值;
(2)若f(x)在x=1取得极值,求函数f(x)的单调区间.
| x2+a |
| x+1 |
(1)若f(x)在点(1,f(1))处的切线斜率为
| 1 |
| 2 |
(2)若f(x)在x=1取得极值,求函数f(x)的单调区间.
(1)f′(x)=
=
,
若f(x)在点(1,f(1))处的切线斜率为
,则f′(1)=
.
所以,f“(1)=
=
,得a=1.
(2)因为f(x)在x=1处取得极值,
所以f'(1)=0,即1+2-a=0,a=3,
∴f′(x)=
.
因为f(x)的定义域为{x|x≠-1},所以有:

所以,f(x)的单调递增区间是(-∞,-3),(1+∞),单调递减区间是(-3,-1),(-1,1).
| 2x(x+1)-x2-a |
| (x+1)2 |
| x2+2x-a |
| (x+1)2 |
若f(x)在点(1,f(1))处的切线斜率为
| 1 |
| 2 |
| 1 |
| 2 |
所以,f“(1)=
| 3-a |
| 4 |
| 1 |
| 2 |
(2)因为f(x)在x=1处取得极值,
所以f'(1)=0,即1+2-a=0,a=3,
∴f′(x)=
| x2+2x-3 |
| (x+1)2 |
因为f(x)的定义域为{x|x≠-1},所以有:

所以,f(x)的单调递增区间是(-∞,-3),(1+∞),单调递减区间是(-3,-1),(-1,1).

练习册系列答案
相关题目
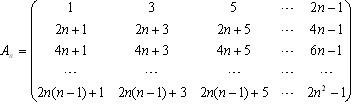 任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则
任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则