题目内容
已知:对于数列{an},定义{△an}为数列{an}的一阶差分数列,其中△an=an+1-an,
(1)若数列{an}的通项公式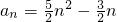 (n∈N*),求:数列{△an}的通项公式;
(n∈N*),求:数列{△an}的通项公式;
(2)若数列{an}的首项是1,且满足△an-an=2n,
①设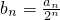 ,求证:数列{bn}是等差数列,并求数列{bn}的通项公式;
,求证:数列{bn}是等差数列,并求数列{bn}的通项公式;
②求:数列{an}的通项公式及前n项和Sn.
解:(1)依题意△an=an+1-an,
∴△an=[ (n+1)2-
(n+1)2- (n+1)]-[
(n+1)]-[ n]=5n+1
n]=5n+1
(2)①由△an-an=2n?an+1-an-an=2n?an+1=2an+2n.
∵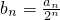 ,
,
∴bn+1-bn= =
= =
= ,且
,且 ,
,
故{bn}是首项为 ,公差为
,公差为 的等差数列
的等差数列
∴bn=
②∵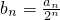 ,
,
∴an= =n•2n-1
=n•2n-1
∴sn=1•20+2×21+3×22+…+n•2n-1(1)
2sn=1•21+2•22+…+n•2n(2)
(1)-(2)得-sn=1+2+22+…+2n-1-n•2n
=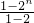 -n•2n
-n•2n
∴sn=n•2n-2n+1
=(n-1)2n+1.
分析:(1)直接把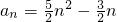 代入△an=an+1-an,整理即可求出数列{△an}的通项公式;
代入△an=an+1-an,整理即可求出数列{△an}的通项公式;
(2)①先利用△an-an=2n得到an+1=2an+2n.再利用等差数列的定义来证明数列{bn}是等差数列即可,进而求出数列{bn}的通项公式;
②由上面求出的结论,直接代入可以得到数列{an}的通项公式,再利用数列求和的错位相减法求和即可.
点评:本题是在新定义下对等差数列的知识以及错位相减法求和的考查,主要考查运算能力.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.
∴△an=[
 (n+1)2-
(n+1)2- (n+1)]-[
(n+1)]-[ n]=5n+1
n]=5n+1(2)①由△an-an=2n?an+1-an-an=2n?an+1=2an+2n.
∵
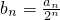 ,
,∴bn+1-bn=
 =
= =
= ,且
,且 ,
,故{bn}是首项为
 ,公差为
,公差为 的等差数列
的等差数列∴bn=

②∵
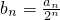 ,
,∴an=
 =n•2n-1
=n•2n-1∴sn=1•20+2×21+3×22+…+n•2n-1(1)
2sn=1•21+2•22+…+n•2n(2)
(1)-(2)得-sn=1+2+22+…+2n-1-n•2n
=
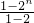 -n•2n
-n•2n∴sn=n•2n-2n+1
=(n-1)2n+1.
分析:(1)直接把
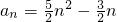 代入△an=an+1-an,整理即可求出数列{△an}的通项公式;
代入△an=an+1-an,整理即可求出数列{△an}的通项公式;(2)①先利用△an-an=2n得到an+1=2an+2n.再利用等差数列的定义来证明数列{bn}是等差数列即可,进而求出数列{bn}的通项公式;
②由上面求出的结论,直接代入可以得到数列{an}的通项公式,再利用数列求和的错位相减法求和即可.
点评:本题是在新定义下对等差数列的知识以及错位相减法求和的考查,主要考查运算能力.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (n∈N*),求:数列{△an}的通项公式;
(n∈N*),求:数列{△an}的通项公式; ,求证:数列{bn}是等差数列,并求数列{bn}的通项公式;
,求证:数列{bn}是等差数列,并求数列{bn}的通项公式;