题目内容
已知两条直线m，n，两个平面α，β，给出下面四个命题：
①
②
③
； ④
其中正确命题的序号是（ ）
| A．① ④ | B．① ③ | C．② ④ | D．② ③ |
A
解析考点：空间中直线与平面之间的位置关系．
分析：由题意用线面垂直和面面平行的定理，判断线面和面面平行和垂直的关系．
解：用线面垂直和面面平行的定理可判断①④正确；
②中，由面面平行的定义，m，n可以平行或异面；
③中，用线面平行的判定定理知，n可以在α内；
故选A．
练习册系列答案
相关题目
已知直线l∥平面α，P∈α，那么过点P且平行于直线l的直线
| A．只有一条，不在平面α内 | B．有无数条，不一定在平面α内 |
| C．只有一条，且在平面α内 | D．有无数条，一定在平面α内 |
下列命题中：
（1）、平行于同一直线的两个平面平行；（2）、平行于同一平面的两个平面平行；
（3）、垂直于同一直线的两直线平行；（4）、垂直于同一平面的两直线平行；
.其中正确的个数有（ ）
| A．1 | B．2 | C．3 | D．4 |
下列说法正确的是（ ）.
| A．一条直线和一个平面平行，它就和这个平面内的任一条直线平行 |
| B．平行于同一平面的两条直线平行 |
| C．如果一个平面内的无数条直线平行于另一个平面，则这两个平面平行 |
| D．如果一个平面内任何一条直线都平行于另一个平面，则这两个平面平行 |
类比平面几何中的定理 “设
是三条直线，若
，则
∥
”，得出如下结论：
①设是空间的三条直线，若，则∥；
②设
是两条直线，
是平面，若
，则∥；
③设
是两个平面，
是直线，若
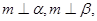则∥
；
④设
是三个平面，若
，则∥；
其中正确命题的个数是（ ）
A． | B． | C． | D． |
的底面是正方形，侧棱
平面 
，且
，则异面直线
所成角的余弦值为（ ）
已知
且
，则
与
的位置关系是 （ ）
A． | B． | C． | D． |
