题目内容
向量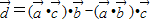 ,若记非零向量
,若记非零向量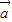 与非零向量
与非零向量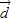 的夹角为θ,则函数
的夹角为θ,则函数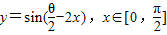 的单调递减区间为 .
的单调递减区间为 .
【答案】分析:先根据向量的数量积得到θ= ;再结合诱导公式以及余弦函数的单调性即可得到结论.
;再结合诱导公式以及余弦函数的单调性即可得到结论.
解答:解:∵ ,
,
∴ •
• =(
=( •
• )•
)• •
• -(
-(
 )•
)• •
•
=( •
• )•(
)•( •
• )-(
)-( •
• )•(
)•( •
• )
)
=0.
又∵ ≠
≠ ,
, ≠
≠ ;
;
∴ ⊥
⊥ ;
;
∴θ= .
.
∴y=sin(θ-2x)=cos2x;
令2kπ≤2x≤2kπ+π⇒kπ≤x≤kπ+ ,k∈Z.
,k∈Z.
与[0, ]取交集得[0,
]取交集得[0, ].
].
故答案为:[0, ].
].
点评:本题主要考查复合函数的单调性以及向量的数量积的运算,关键是利用余弦函数的单调性,整体思考,考查计算能力,是中档题.
 ;再结合诱导公式以及余弦函数的单调性即可得到结论.
;再结合诱导公式以及余弦函数的单调性即可得到结论.解答:解:∵
 ,
,∴
 •
• =(
=( •
• )•
)• •
• -(
-(
 )•
)• •
•
=(
 •
• )•(
)•( •
• )-(
)-( •
• )•(
)•( •
• )
)=0.
又∵
 ≠
≠ ,
, ≠
≠ ;
;∴
 ⊥
⊥ ;
;∴θ=
 .
.∴y=sin(θ-2x)=cos2x;
令2kπ≤2x≤2kπ+π⇒kπ≤x≤kπ+
 ,k∈Z.
,k∈Z.与[0,
 ]取交集得[0,
]取交集得[0, ].
].故答案为:[0,
 ].
].点评:本题主要考查复合函数的单调性以及向量的数量积的运算,关键是利用余弦函数的单调性,整体思考,考查计算能力,是中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
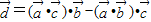 ,若记非零向量
,若记非零向量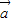 与非零向量
与非零向量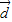 的夹角为θ,则函数
的夹角为θ,则函数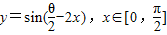 的单调递减区间为 .
的单调递减区间为 .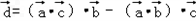 ,若记非零向量
,若记非零向量 与非零向量
与非零向量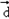 的夹角为θ,则函数
的夹角为θ,则函数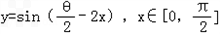 的单调递减区间为( )
的单调递减区间为( )