题目内容
(1)已知实数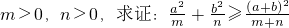 ;
;
(2)利用(1)的结论,求函数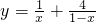 (其中x∈(0,1))的最小值.
(其中x∈(0,1))的最小值.
证明:(1)∵m>0 且n>0,
= =
= ≥0
≥0
所以 当且仅当na=mb时等号成立
当且仅当na=mb时等号成立
(2)∵x∈(0,1),∴1-x>0,
∴

由(1-x)•1=x•2,可得 ,
,
故当 时,函数可得最小值 9.
时,函数可得最小值 9.
分析:(1)由已知条件,把要证的不等式的左边减去右边通分化简为
 ,显然此值大于0,故不等式成立.
,显然此值大于0,故不等式成立.(2)把函数解析式化为
 ,利用(1)的结论,可得它大于或等于
,利用(1)的结论,可得它大于或等于 =9,由此得出结论.
=9,由此得出结论.点评:本题主要考查用综合法证明不等式,基本不等式的应用,式子的变形是解题的关键,属于中档题.

练习册系列答案
相关题目
 ;
; (其中x∈(0,1))的最小值.
(其中x∈(0,1))的最小值.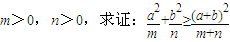 ;
;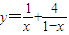 (其中x∈(0,1))的最小值.
(其中x∈(0,1))的最小值.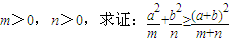 ;
;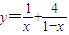 (其中x∈(0,1))的最小值.
(其中x∈(0,1))的最小值.