Question

【题目】已知函数，.

（1）若函数恰有一个极值点，求实数a的取值范围；

（2）当，且时，证明：.（常数是自然对数的底数）.

Answer 1

【答案】（1）（2）证明见解析

【解析】

1，等价于方程在恰有一个变号零点．

即在恰有一个变号零点．令，利用函数图象即可求解．

2要证明：只需证明，即证明要证明，即证明利用导数即可证明．

Ⅰ，，

，

函数恰有一个极值点，

方程在恰有一个变号零点．

在恰有一个变号零点．

令，则．

可得时，，函数单调递增，

时，，函数单调递减．

函数草图如下，

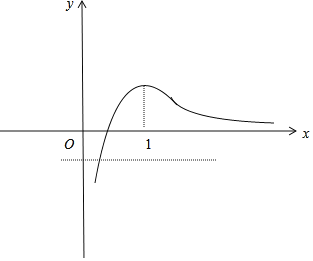
可得，

．

实数a的取值范围为：

2要证明：证明．

证明，即证明．

令则，

时，，函数递增，时，，递减．

，即原不等式成立．

要证明，即证明．

，

故只需证明即可．

令，则．

时，，函数递减，时，，函数递增．

，

又，

故原不等式成立．

综上，，