题目内容
(本题满分14分)如图，正方形ABCD和四边形ACEF所在的平面互相垂直
EF//AC，AB=
,CE=EF=1
（Ⅰ）求证：AF//平面BDE
（Ⅱ）求证：CF⊥平面BDE;
证明：（Ⅰ）设AC于BD交于点G。因为EF∥AG,且EF=1，AG=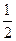
AG=1
所以四边形AGE
F为平行四边形
所以AF∥EG
因为EG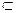
平面BDE,AF
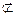平面BDE,
所以AF∥平面BDE 
7分
（Ⅱ）连接FG。因为EF∥CG,EF=CG=1,且CE=1
,所以平行四边形CE
FG为菱形
所以CF⊥EG.
因为四边形ABCD为正方形，所以BD⊥AC.
又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG=G,所以CF⊥平面BDE. 14分
解析
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
，E是棱CC1上动点，F是AB中点，
；
、
的边长都是1，平面
平面
在
上移动，点
在
上移动，若
（
）
的长；
为何值时，
与面
所成锐二面角余弦值的大小.
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
平面C1CBB1；