Question

如图，在△ABC中，∠BAC=60°，线段AD⊥平面ABC，AH⊥平面DBC，H为垂足.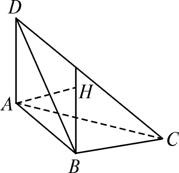

求证：H不可能是△BCD的垂心.

Answer 1

解析：证明“不可能”无法下手，从反面“可能”考虑，用反证法证明.

证明：假设H是△BCD的垂心，则BH⊥CD.

∵AH⊥平面DBC，DC平面DBC，∴AH⊥DC.

∵AH∩BH＝H,∴CD⊥平面ABH.

又AB平面ABH,∴CD⊥AB.

∵AD⊥平面ABC，AB平面ABC,∴AD⊥AB.

由于AD∩CD＝D,∴AB⊥平面ACD.

∵AC平面ACD,∴AB⊥AC.这与已知中∠BAC＝60°相矛盾.

∴假设不成立.故H不可能是△BCD的垂心.

点评：(1)“不可能”类型的问题用反证法证明.“不可能”的反面是“可能”.

(2)注意反证法的证题过程.实际上∠BAC只要不是90°，这个题型的方法总是一样的.