题目内容
(本小题满分12分)定义在区间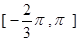 上的函数
上的函数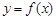 的图象关于直线
的图象关于直线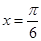 对称,当
对称,当
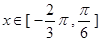 时函数
时函数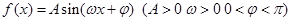 图象如图所示.
图象如图所示.
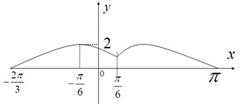
(1)求函数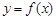 在
在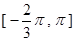 的表达式;
的表达式;
(2)求方程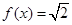 的解;
的解;
(3)是否存在常数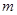 的值,使得
的值,使得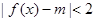 在
在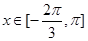 上恒成立;若存在,求出
上恒成立;若存在,求出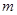 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
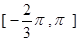 上的函数
上的函数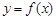 的图象关于直线
的图象关于直线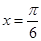 对称,当
对称,当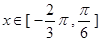 时函数
时函数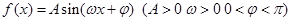 图象如图所示.
图象如图所示.
(1)求函数
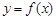 在
在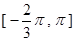 的表达式;
的表达式;(2)求方程
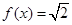 的解;
的解;(3)是否存在常数
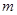 的值,使得
的值,使得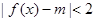 在
在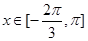 上恒成立;若存在,求出
上恒成立;若存在,求出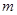 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.(1) ;(2)
;(2)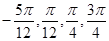 ;(3)存在,
;(3)存在,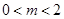 .
.
 ;(2)
;(2)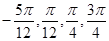 ;(3)存在,
;(3)存在, .
.试题分析:(1)当
 时,由图象可求得
时,由图象可求得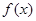 ,由
,由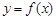 的图象关于直线
的图象关于直线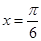 对称,则
对称,则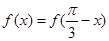 ,当
,当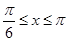 时,易求
时,易求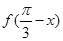 ;(2)分
;(2)分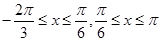 两种情况进行讨论可解方程;(3)由条件
两种情况进行讨论可解方程;(3)由条件 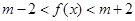 在
在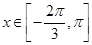 上恒成立,可转化为函数的最值解决,而最值可借助图象求得.
上恒成立,可转化为函数的最值解决,而最值可借助图象求得.试题解析:(1)
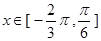 ,
,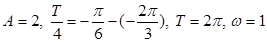 且
且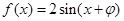 过
过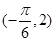 ,∵
,∵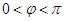 ∴
∴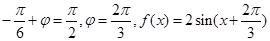 当
当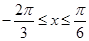
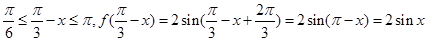 而函数
而函数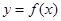 的图象关于直线
的图象关于直线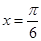 对称,则
对称,则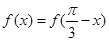 即
即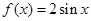 ,
,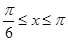
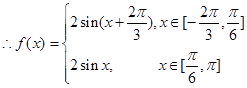
当
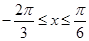 时,
时,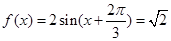
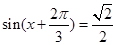 ∴
∴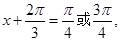
即
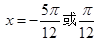 ,当
,当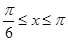 时,
时,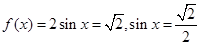 ∴
∴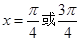 ∴方程
∴方程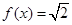 的解集是
的解集是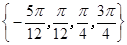 ;(3)存在假设存在,由条件得
;(3)存在假设存在,由条件得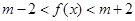 在
在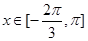 上恒成立即
上恒成立即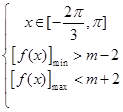 ,由图象可得
,由图象可得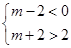 ∴
∴ 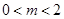 .
.
练习册系列答案
相关题目
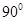 的角是第象Ⅰ限角;
的角是第象Ⅰ限角;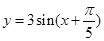 的图象上所有点向左平移
的图象上所有点向左平移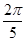 个单位长度可得到
个单位长度可得到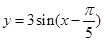 的图象;
的图象;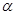 、
、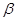 是第Ⅰ象限角,且
是第Ⅰ象限角,且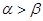 ,则
,则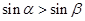 ;
;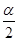 是第Ⅰ或第Ⅲ象限的角;
是第Ⅰ或第Ⅲ象限的角;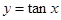 在整个定义域内是增函数
在整个定义域内是增函数 
 ,求
,求 的值;
的值; ,若
,若 ,求
,求 的值.
的值.  ,其中
,其中
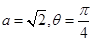 时,求
时,求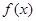 在区间
在区间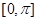 上的最大值与最小值;
上的最大值与最小值;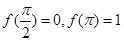 ,求
,求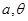 的值.
的值.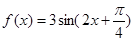 有以下命题,其中正确的个数( )
有以下命题,其中正确的个数( )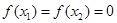 ,则
,则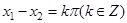 ;②
;②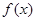 图象与
图象与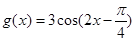 图象相同;③
图象相同;③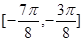 上是减函数;④
上是减函数;④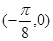 对称.
对称.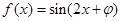 ,其中
,其中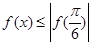 对
对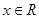 恒成立,且
恒成立,且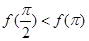 ,则
,则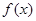 的单调递增区间是( )
的单调递增区间是( )
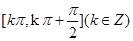
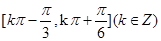
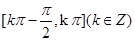
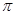 ]内,满足sinx>cosx的x的取值范围是( )
]内,满足sinx>cosx的x的取值范围是( ) ,
,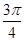 )
) )
)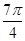 )
) ,向量
,向量 ,则
,则 的最大值、最小值分别是( ).
的最大值、最小值分别是( ).



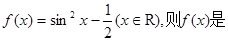 ( ).
( ).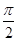 的奇函数
的奇函数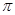 的奇函数
的奇函数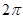 的偶函数
的偶函数