题目内容

如图,A1B1C1—ABC是直三棱柱,过A1、B、C1的平面和平面ABC的交线为l.

(1)判定l与直线A1C1的位置关系,并给出证明;

(2)当AA1=1,AB=4,BC=3,∠ABC=90°时,求A1到l的距离.

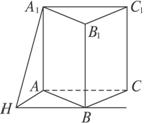
解析:(1)∵A1C1∥AC,A1C1平面A1B1C1,AC平面ABC,

∴A1C1∥平面ABC.又平面A1BC1与平面ABC的交线为l,于是A1C1∥l.

(2)过A作AH⊥l于H,连结A1H,则AH是A1H在平面ABC上的射影,

于是A1H垂直于直线l,A1H的长为A1到l的距离,又AH等于B到AC的距离等于.

故在Rt△A1AH中,A1H=.

练习册系列答案
相关题目
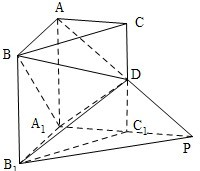精英家教网如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1=1，D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA1
（Ⅰ）求证：CD=C1D；
（Ⅱ）求二面角A-A1D-B的平面角的余弦值；
（Ⅲ）求点C到平面B1DP的距离．
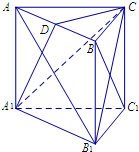精英家教网如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=BB1=2，D为AB的中点．
（Ⅰ）求证：BC1∥平面A1CD；
（Ⅱ）求证：BC1⊥平面AB1C；
（Ⅲ）求三棱锥D-A1AC的体积．
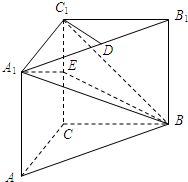精英家教网如图，在三棱柱ABC-A1B1C1中，B1B⊥平面A1B1C1AC=CB=CC1=2，∠ACB=90°，D，E分别是A1B1，CC1的中点．
（Ⅰ）求证：C1D∥平面A1BE；
（Ⅱ）求证：平面A1BE⊥平面AA1B1B；
（Ⅲ）求直线BC1与平面A1BE所成角的正弦值．
精英家教网如图，三棱柱ABC-A1B1C1中，侧棱与底面ABC垂直，且AB1⊥BC1，AB=AA1=1，BC=2．
（I）证明：A1C1⊥AB；
（II）求二面角A1-BC1-A的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网