题目内容
设函数f(x)=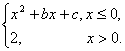 若 f(-4)=f(0),f(-2)=-2,则关于x的方程f(x)=x的解的个数为( )
若 f(-4)=f(0),f(-2)=-2,则关于x的方程f(x)=x的解的个数为( )A.1 B.2 C.3 D.4
解:由f(-4)=f(0),f(-2)=-2,得16-4b+c=c且4-2b+c=-2.
解得b=4,c=2,所以f(x)=x2+4x+2(x≤0).若f(x)=x2+4x+2=x,
即x2+3x+2= 0,解得x=-1或x=-2,满足题意.又由于当x>0时,f(x)=2,所以有f(2)=2,因此满足条件的解的个数只有三个.
答案:C

练习册系列答案
相关题目
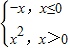 ,若f(a)=4,则实数a=( )
,若f(a)=4,则实数a=( )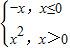 ,若f(a)=4,则实数a=( )
,若f(a)=4,则实数a=( )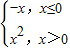 ,若f(a)=4,则实数a=( )
,若f(a)=4,则实数a=( ) ,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)= ,关于x的方程f(x)=x的解的个数为 .
,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)= ,关于x的方程f(x)=x的解的个数为 .