题目内容
13.温江某农户计划种植蒜台和花菜,种植面积不超过50亩,投入资金不超过54万元,假设种植蒜台和菜花的产量、成本和价格如表所示:| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 蒜台 | 4吨 | 1.2万元 | 0.55万元 |
| 花菜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50万 | B. | 48万 | C. | 47万 | D. | 45万 |
分析 由题意,设农户计划种植蒜台和花菜分别x亩,y亩;从而可得约束条件以及目标函数总利润z=0.55×4x+0.3×6y-(1.2x+0.9y)=x+0.9y;从而由线性规划求最优解即可
解答 解:设农户计划种植蒜台和花菜各x亩,y亩;
则由题意可得,$\left\{\begin{array}{l}{x+y≤50}\\{1.2x+0.9y≤54}\\{x,y≥0}\end{array}\right.$;
一年的种植总利润z=0.55×4x+0.3×6y-(1.2x+0.9y)=x+0.9y;
作平面区域如下,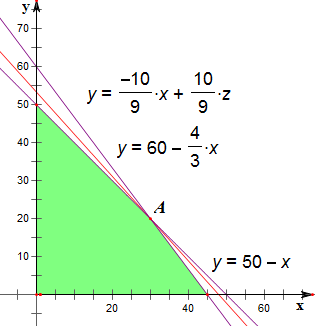
结合图象可知,
$\left\{\begin{array}{l}{y=60-\frac{4}{3}x}\\{y=50-x}\end{array}\right.$;
解得x=30,y=20;此时一年的种植总利润最大为30+0.9×20=48;
故选:B.
点评 本题考查了线性规划在实际问题中的应用及学生的作图能力,关键是正确列出约束条件以及目标函数,利用简单线性规划解决最优解问题;属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
3.正方体ABCD-A1B1C1D1中,M是DD1的中点,O为底面ABCD的中心,P为棱A1B1上的任意一点,则直线OP与直线AM所成的角为( )
| A. | 45° | B. | 60° | C. | 90° | D. | 与点P的位置有关 |
1.若点P的极坐标为(2$\sqrt{3}$,$\frac{2π}{3}$),则点P的直角坐标为( )
| A. | (-$\sqrt{3}$,3) | B. | (-3,$\sqrt{3}$) | C. | (3,-$\sqrt{3}$) | D. | ($\sqrt{3}$,-3) |
18.已知{an}是等比数列,{bn}是等差数列,若a2•a14=4a8,b8=a8,则数列{bn}的前15项和等于( )
| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
5.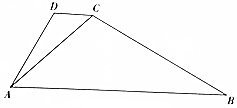 如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=$\sqrt{6}$-$\sqrt{2}$.
如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=$\sqrt{6}$-$\sqrt{2}$.
(Ⅰ)求AD的长;
(Ⅱ)若BC=$\sqrt{10}$,求△ABC的面积.
 如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=$\sqrt{6}$-$\sqrt{2}$.
如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=$\sqrt{6}$-$\sqrt{2}$.(Ⅰ)求AD的长;
(Ⅱ)若BC=$\sqrt{10}$,求△ABC的面积.
2.$sin\frac{5π}{3}$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
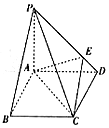 如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.
如图,点P是边长为1的正方形ABCD所在平面外一点,PA⊥CD,PA=1,PD=$\sqrt{2}$,E为PD上一点,PE=2ED.