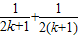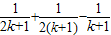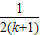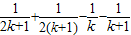题目内容
对任意大于或等于2的正整数都成立的不等式：
+
+
+…+
＞
，当n=k+1时其左端与n=k时其右端所相差的式子是（其中k∈Z，k≥2）（ ）
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 13 |
| 24 |
A．
| B．
| ||||||||||
C．
| D．
|
当n=k时左端为
+
+
+…+
，
当n=k+1时其左端为
+
+
…+
+
+
，
故当n=k+1时其左端的式子与当n=k时左端的式子的差为
+
-
，
故选B．
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
当n=k+1时其左端为
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| k+4 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
故当n=k+1时其左端的式子与当n=k时左端的式子的差为
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
| 1 |
| k+1 |
故选B．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
对任意大于或等于2的正整数都成立的不等式：
+
+
+…+
＞
，当n=k+1时其左端与n=k时其右端所相差的式子是（其中k∈Z，k≥2）（ ）
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 13 |
| 24 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
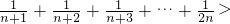
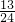，当n=k+1时其左端与n=k时其右端所相差的式子是（其中k∈Z，k≥2）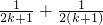
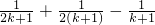
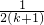
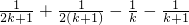
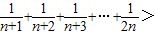
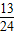，当n=k+1时其左端与n=k时其右端所相差的式子是（其中k∈Z，k≥2）（ ）
