题目内容
已知过点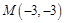 的直线
的直线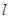 与圆
与圆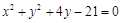 相交于
相交于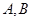 两点,若弦
两点,若弦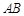 的长为
的长为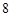 ,求直线
,求直线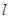 的方程;
的方程;
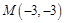 的直线
的直线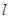 与圆
与圆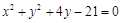 相交于
相交于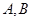 两点,若弦
两点,若弦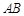 的长为
的长为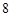 ,求直线
,求直线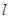 的方程;
的方程; 和
和 .............12分
.............12分把圆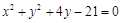 ,写成标准式得
,写成标准式得 。所以圆心
。所以圆心 ,半径
,半径 。利用半径
。利用半径 ,弦
,弦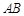 的长的二分之一为4,得圆心
的长的二分之一为4,得圆心 到直线
到直线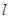 的距离为3,讨论过点
的距离为3,讨论过点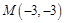 的直线斜率是否存在,可求出直线
的直线斜率是否存在,可求出直线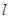 的方程。
的方程。
解:若直线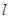 的斜率不存在,则
的斜率不存在,则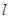 的方程为
的方程为 ,此时有
,此时有 ,弦
,弦 ,所以合题意...............2分
,所以合题意...............2分
故设直线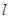 的方程为
的方程为 ,即
,即 ............4分
............4分
将圆的方程写成标准式得 ,
,
所以圆心 ,半径
,半径 .....................6分
.....................6分
圆心 到直线
到直线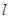 的距离
的距离 ,
,
即 ,............................10分
,............................10分
所求直线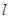 的方程为
的方程为 和
和 .............12分
.............12分
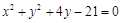 ,写成标准式得
,写成标准式得 。所以圆心
。所以圆心 ,半径
,半径 。利用半径
。利用半径 ,弦
,弦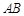 的长的二分之一为4,得圆心
的长的二分之一为4,得圆心 到直线
到直线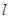 的距离为3,讨论过点
的距离为3,讨论过点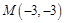 的直线斜率是否存在,可求出直线
的直线斜率是否存在,可求出直线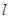 的方程。
的方程。解:若直线
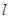 的斜率不存在,则
的斜率不存在,则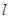 的方程为
的方程为 ,此时有
,此时有 ,弦
,弦 ,所以合题意...............2分
,所以合题意...............2分故设直线
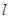 的方程为
的方程为 ,即
,即 ............4分
............4分将圆的方程写成标准式得
 ,
,所以圆心
 ,半径
,半径 .....................6分
.....................6分圆心
 到直线
到直线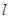 的距离
的距离 ,
,即
 ,............................10分
,............................10分所求直线
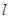 的方程为
的方程为 和
和 .............12分
.............12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
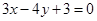 与圆
与圆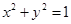 相交所截的弦长为( )
相交所截的弦长为( )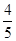
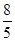
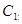
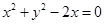 与圆
与圆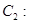
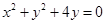 的位置关系为 .
的位置关系为 .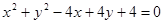 上有四点到直线
上有四点到直线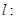
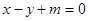 的距离为
的距离为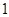 ,则
,则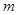 的取值范围为______________.
的取值范围为______________.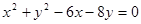 ,过坐标原点作长为8的弦,求弦所在直线的方程.
,过坐标原点作长为8的弦,求弦所在直线的方程.
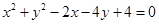 相交所得弦的长为2,则该直线的方程为________;
相交所得弦的长为2,则该直线的方程为________;  上一点
上一点 的切线方程是____________.
的切线方程是____________.