题目内容
(2007•武汉模拟)(1)已知函数m(x)=ax2e-x (a>0),求证:函数y=m(x)在区间[2,+∞)上为减函数.
(2)已知函数f(x)=ax2+2ax,g(x)=ex,若在(0,+∞)上至少存在一点x0,使得f(x0)>g(x0)成立,求实数a的取值范围.
(2)已知函数f(x)=ax2+2ax,g(x)=ex,若在(0,+∞)上至少存在一点x0,使得f(x0)>g(x0)成立,求实数a的取值范围.
分析:(1)欲证函数y=m(x)在区间[2,+∞)上为减函数,求出导函数f′(x),只须证明f′(x)<0即可;
(2)欲在(0,+∞)上至少存在一点x0,使f(x0)>g(x0)成立,只需f(x)=
的最大值大于1,建立不等关系,解之即可.
(2)欲在(0,+∞)上至少存在一点x0,使f(x0)>g(x0)成立,只需f(x)=
| f(x) |
| g(x) |
解答:解:(1)m'(x)=axe-x(2-x),而ax>0,∴当x>2时,m'(x)<0,因此m(x)在[2,+∞)上为减函数.
(2)记m(x)=
,则m'(x)=(-ax2+2a)e-x,
当x>
时,m'(x)<0 当0<x<
时,m'(x)>0
故m(x)在x=
时取最大值,同时也为最大值.m(x)max=m(
)=
依题意,要在(0,+∞)上存在一点x0,使f(x0)>g(x0)成立.即使m(x0)>1只需m(
)>1
即
>1∴a>
e
,因此,所求实数a的取值范围为(
e
,+∞)
(2)记m(x)=
| ax2+2ax |
| ex |
当x>
| 2 |
| 2 |
故m(x)在x=
| 2 |
| 2 |
2a+2
| ||
e
|
依题意,要在(0,+∞)上存在一点x0,使f(x0)>g(x0)成立.即使m(x0)>1只需m(
| 2 |
即
2a+2
| ||
e
|
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查利用导数研究函数的单调性,利用导数求闭区间上函数的最值等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
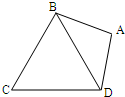 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=