题目内容
已知a,b,分别是△ABC中角A,B,C的对边,且sin2A+sin2C-sin2b=sinAsinC
(1)求角B的大小;
(2)若△ABC的面积为
,且b=
,求a+c的值.
(1)求角B的大小;
(2)若△ABC的面积为
3
| ||
| 4 |
| 3 |
(1)∵sin2A+sin2C-sin2b=sinAsinC,
∴由正弦定理,得a2+c2-b2=ac
再由余弦定理,得cosB=
=
,
∵B∈(0,π),∴B=
.
(2)∵△ABC的面积为
,
∴
acsinB=
,即
acsin
=
,可得ac=3.
∵b=
,得b2=a2+c2-2accosB,即a2+c2-ac=3.
两边都加上3ac,得a2+c2+2ac=12
即(a+c)2=12,可得a+c=2
.
∴由正弦定理,得a2+c2-b2=ac
再由余弦定理,得cosB=
| a2+b2-c2 |
| 2ac |
| 1 |
| 2 |
∵B∈(0,π),∴B=
| π |
| 3 |
(2)∵△ABC的面积为
3
| ||
| 4 |
∴
| 1 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
| π |
| 3 |
3
| ||
| 4 |
∵b=
| 3 |
两边都加上3ac,得a2+c2+2ac=12
即(a+c)2=12,可得a+c=2
| 3 |

练习册系列答案
相关题目
 如图,已知A、B两点分别是椭圆C:
如图,已知A、B两点分别是椭圆C: 中,已知a、b、
中,已知a、b、 分别是三内角
分别是三内角 、
、 、
、 所对应的边长,且
所对应的边长,且 .
. ,且△
,且△ ,求
,求 的值.
的值. 中,已知a、b、
中,已知a、b、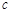 分别是三内角
分别是三内角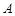 、
、 、
、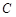 所对应的边长,且
所对应的边长,且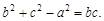
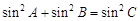 ,试判断△ABC的形状并求角
,试判断△ABC的形状并求角 的左顶点和上顶点,而F是椭圆C的右焦点,若
的左顶点和上顶点,而F是椭圆C的右焦点,若 ,则椭圆C的离心率e= .
,则椭圆C的离心率e= .