题目内容
2012·江苏卷] 如图1-4,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
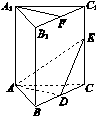
图1-4
证明:(1)因为ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC,
又AD⊂平面ABC,所以CC1⊥AD.
又因为AD⊥DE,CC1,DE⊂平面BCC1B1,CC1∩DE=E,
所以AD⊥平面BCC1B1.又AD⊂平面ADE,
所以平面ADE⊥平面BCC1B1.
(2)因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.
因为CC1⊥平面A1B1C1,且A1F⊂平面A1B1C1,
所以CC1⊥A1F.
又因为CC1,B1C1⊂平面BCC1B1,CC1∩B1C1=C1,
所以A1F⊥平面BCC1B1.
由(1)知AD⊥平面BCC1B1,所以A1F∥AD.
又AD⊂平面ADE,A1F⊄平面ADE,所以A1F∥平面ADE.

练习册系列答案
相关题目

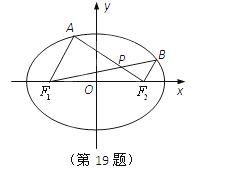 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆