题目内容
如图,在直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
(1)求直线BE与A1C的夹角.
(2)线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出|![]() |,若不存在,请说明理由.
|,若不存在,请说明理由.
解:(1)以B为坐标原点,建立如下图所示的空间直角坐标系B-xyz.

因为AC=2a,∠ABC=90°,
所以AB=BC=![]() a.
a.
所以B(0,0,0),A(![]() a,0,0),C(0,
a,0,0),C(0,![]() a,0),B1(0,0,3a),A1(
a,0),B1(0,0,3a),A1(![]() a,0,3a),C1(0,
a,0,3a),C1(0,![]() a,3a),D(
a,3a),D(![]() a,
a,![]() a,3a),E(0,
a,3a),E(0,![]() a,
a,![]() a),
a),![]() =(
=(![]() a,-
a,-![]() a,3a),
a,3a),![]() =(0,
=(0,![]() a,
a,![]() a).
a).
所以|![]() |=
|=![]() a,|
a,|![]() |=
|=![]() a,
a,
![]() ·
·![]() =0-a2+
=0-a2+![]() a2=
a2=![]() a2.
a2.
所以cos(![]() ,
,![]() )=
)=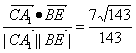 .
.
所以BE与A1C的夹角为arccos![]() .
.
(2)假设存在F点,使CF⊥平面B1DF.不妨设AF=b,则F(2a,0,b),
![]() =(
=(![]() a,-
a,-![]() a,b),
a,b),![]() =(
=(![]() a,0,b-3a),
a,0,b-3a),![]() =(
=(![]() a,
a,![]() a,0).
a,0).
因为![]() ·
·![]() =a2-a2+0=0,
=a2-a2+0=0,
所以![]() ⊥
⊥![]() 恒成立.
恒成立.
由![]() ·
·![]() =2a2+b(b-3a)
=2a2+b(b-3a)
=b2-3ab+2a2=0,
得b=a或b=2a.
所以当|![]() |=a或|
|=a或|![]() |=2a时,CF⊥平面B1DF.
|=2a时,CF⊥平面B1DF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




