题目内容
如图，已知椭圆：
，过点F（4，0）作两条互相垂直的弦AB，CD，设弦AB，CD的中点分别为M，N．（1）线段MN是否恒过一个定点？如果经过定点，试求出它的坐标，如果不经过定点，试说明理由；
（2）求分别以AB，CD为直径的两圆公共弦中点的轨迹方程．
【答案】分析：（1）设出直线AB的方程，代入椭圆方程消去x，设A，B的坐标，根据韦达定理可求得y1+y2的表达式，根据直线方程可求得x1+x2的表达式，进而可求得点M的坐标，根据AB⊥CD，将t换成
，即可求得N的坐标，进而可求得MN的直线方程，把y=0代入直线方程求得x=
进而可推断出直线MN横过
．
（2）根据（1）可表示出以AB为直径的圆的方程，进而依据AB⊥CD，将t换成
，即可表示出直线CD的方程，两方程相减即可求得公共弦所在的方程，与直线MN方程联解消去
即可求得x和y的关系是，即以AB，CD为直径的两圆公共弦中点的轨迹方程．
解答：解：（1）设直线AB的方程为：
并整理得：
（9t2+25）y2+72ty-81=0．
设A（x1，y1），B（x2，y2），则有：
，
所以点
∵AB⊥CD，
∴将t换成
，即得：
由两点式得直线MN的方程为
当y=0时，
，所以直线MN恒过定点
．
（2）以弦AB为直径的圆M的方程为：
①
又∵AB⊥CD，
∴将t换成
，即得以弦CD为直径的圆N的方程为：
②
①-②得两圆公共弦所在直线方程为：
③
又直线MN的方程为：
④
联解③④，消去
，得两圆公共弦中点的轨迹方程为：
．
其轨迹是过定点
的圆．
点评：本题主要考查了直线与圆锥曲线的综合问题．考查了考生分析推理和基本的运算能力．
，即可求得N的坐标，进而可求得MN的直线方程，把y=0代入直线方程求得x=进而可推断出直线MN横过．（2）根据（1）可表示出以AB为直径的圆的方程，进而依据AB⊥CD，将t换成
，即可表示出直线CD的方程，两方程相减即可求得公共弦所在的方程，与直线MN方程联解消去即可求得x和y的关系是，即以AB，CD为直径的两圆公共弦中点的轨迹方程．解答：解：（1）设直线AB的方程为：
并整理得：（9t2+25）y2+72ty-81=0．
设A（x1，y1），B（x2，y2），则有：
，所以点
∵AB⊥CD，
∴将t换成
，即得：由两点式得直线MN的方程为
当y=0时，
，所以直线MN恒过定点．（2）以弦AB为直径的圆M的方程为：
①又∵AB⊥CD，
∴将t换成
，即得以弦CD为直径的圆N的方程为：②①-②得两圆公共弦所在直线方程为：
③又直线MN的方程为：
④联解③④，消去
，得两圆公共弦中点的轨迹方程为：．其轨迹是过定点
的圆．点评：本题主要考查了直线与圆锥曲线的综合问题．考查了考生分析推理和基本的运算能力．
练习册系列答案
应用题作业本系列答案
相关题目
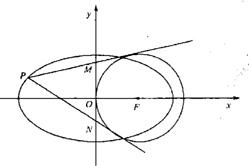如图，已知椭圆
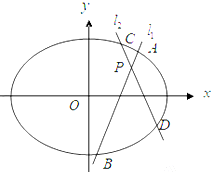如图，已知椭圆
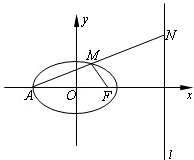如图，已知椭圆
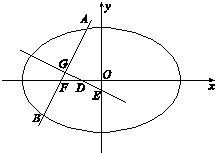（2013•甘肃三模）如图，已知椭圆