题目内容
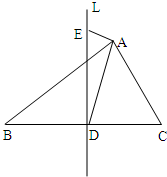 如图,在△ABC中,
如图,在△ABC中,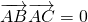 ,
, ,L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
,L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
(1)求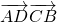 的值.
的值.
(2)判断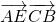 的值是否为一个常数,并说明理由.
的值是否为一个常数,并说明理由.
解:法1:(1)由已知可得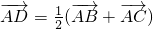 ,
,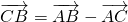 ,
,
∴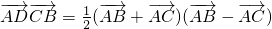
=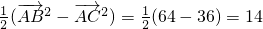
(2)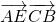 的值为一个常数∵L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
的值为一个常数∵L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
∴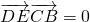 ,
,
故: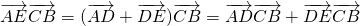 =
=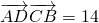
解法2:(1)以D点为原点,BC所在直线为X轴,L所在直线为Y轴建立直角坐标系,可求A(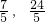 ),
),
此时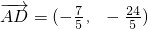 ,
,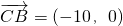 ,
,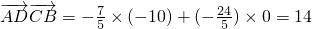
(2)设E点坐标为(0,y)(y≠0),
∴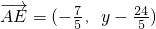 ,
,
∴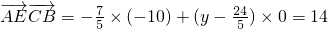 (常数).
(常数).
分析:法一:(1)由题意及图形,可把向量 用两个向量
用两个向量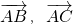 的表示出来,再利用数量积的公式求出数量积;
的表示出来,再利用数量积的公式求出数量积;
(2)将向量 用
用 与
与 表示出来,再由向量的数量积公式求数量积,根据其值的情况确定是否是一个常数;
表示出来,再由向量的数量积公式求数量积,根据其值的情况确定是否是一个常数;
法二:(1)由题意可以以BC所在直线为X轴,DE所在直线为Y轴建立坐标系,得出各点的坐标,由向量坐标的定义式求出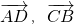 的坐标表示,由向量的数量积公式求数量积;
的坐标表示,由向量的数量积公式求数量积;
(2)设E点坐标为(0,y)(y≠0),表示出向量 的坐标再由向量的数量积坐标表示公式求数量积即可
的坐标再由向量的数量积坐标表示公式求数量积即可
点评:本题考查向量在几何中的应用,本题采用了二种解法,一是基向量法,一是向量的坐标表示,解题的关键是建立坐标系与设定其向量
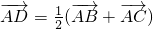 ,
,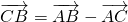 ,
,∴
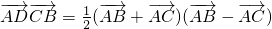
=
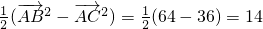
(2)
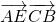 的值为一个常数∵L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,
的值为一个常数∵L为L为线段BC的垂直平分线,L与BC交与点D,E为L上异于D的任意一点,∴
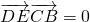 ,
,故:
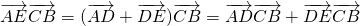 =
=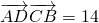
解法2:(1)以D点为原点,BC所在直线为X轴,L所在直线为Y轴建立直角坐标系,可求A(
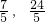 ),
),此时
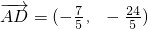 ,
,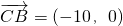 ,
,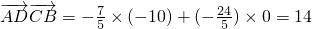
(2)设E点坐标为(0,y)(y≠0),
∴
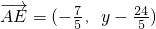 ,
,∴
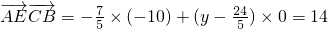 (常数).
(常数).分析:法一:(1)由题意及图形,可把向量
 用两个向量
用两个向量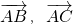 的表示出来,再利用数量积的公式求出数量积;
的表示出来,再利用数量积的公式求出数量积;(2)将向量
 用
用 与
与 表示出来,再由向量的数量积公式求数量积,根据其值的情况确定是否是一个常数;
表示出来,再由向量的数量积公式求数量积,根据其值的情况确定是否是一个常数;法二:(1)由题意可以以BC所在直线为X轴,DE所在直线为Y轴建立坐标系,得出各点的坐标,由向量坐标的定义式求出
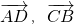 的坐标表示,由向量的数量积公式求数量积;
的坐标表示,由向量的数量积公式求数量积;(2)设E点坐标为(0,y)(y≠0),表示出向量
 的坐标再由向量的数量积坐标表示公式求数量积即可
的坐标再由向量的数量积坐标表示公式求数量积即可点评:本题考查向量在几何中的应用,本题采用了二种解法,一是基向量法,一是向量的坐标表示,解题的关键是建立坐标系与设定其向量

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知