题目内容
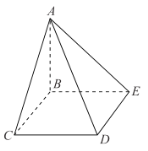
【题目】如图1,在梯形ABCD中,
,
,
,过A,B分别作CD的垂线,垂足分别为E,F,已知
,
,将梯形ABCD沿AE,BF同侧折起,使得平面
平面ABFE,平面
平面BCF,得到图2.
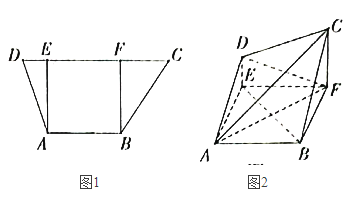
（1）证明:
平面ACD;
（2）求二面角
的余弦值.
【答案】（1）证明见解析.（2）
【解析】
（1）设
,取AC中点M,连接OM，DM，可证明四边形DEOM为平行四边形 可得
，即得证；
（2）建立如图空间直角坐标系，求解平面ADF，平面ADC的法向量，由二面角的向量公式即得解.
（1）设,取AC中点M,连接OM，DM
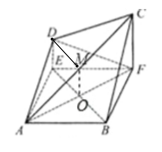
四边形ABFE为正方形 ∴为AF中点 ∵M为AC中点 ∴
∵平面
平面ABFE
平面
平面
平面ABFE
平面ADE
又∵平面
平面BCF
∴平面
平面ABFE 同理,
平面ABFE
又∵
,
∴
∴
∴四边形DEOM为平行四边形 ∴
∵
平面ADC,
平面ADC
∴
（2）由题意EA，EF，ED两两垂直，以EA为x轴,EF为y轴,ED为z轴建立空间直角坐标系
∴
,
,
,
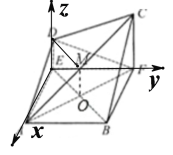
设平面ADF的法向量为
∵
,
∴
∴
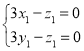
设平面ADC的法向量为
∵
∴
∴
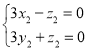
设二面角
的平面角为θ,由图像得θ为锐角，
∴
练习册系列答案
相关题目
【题目】某同学用“五点法”画函数
在某一个周期内的图象时，列表并填入了部分数据，如下表：
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
（1）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数
的解析式；
（2）将
图象上所有点向左平行移动
个单位长度，并把图象上所有点的横坐标缩短为原来的
（纵坐标不变），得到
的图象.若
图象的一个对称中心为
，求
的最小值；
（3）在（2）条件下，求
在
上的增区间.
