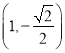题目内容
【题目】【广东省惠州市2017届高三上学期第二次调研】已知点![]() ,点
,点![]() 是圆
是圆![]()
![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若直线![]() 与点
与点![]() 的轨迹有两个不同的交点
的轨迹有两个不同的交点![]() 和
和![]() ,且原点
,且原点![]() 总在以
总在以![]() 为直径的圆的内部,求实数
为直径的圆的内部,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)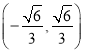
【解析】
试题分析:(Ⅰ)求动点轨迹方程,由题意动点E满足![]() ,轨迹是椭圆,由椭圆标准方程可得结论;(Ⅱ)原点
,轨迹是椭圆,由椭圆标准方程可得结论;(Ⅱ)原点![]() 总在以
总在以![]() 为直径的圆的内部,即∠POQ大于90°,反应在数量上就是
为直径的圆的内部,即∠POQ大于90°,反应在数量上就是![]() ,
,
因此设设![]() ,
,![]() ,把直线与椭圆的方程联立消去y得x的一元二次方程,从而得
,把直线与椭圆的方程联立消去y得x的一元二次方程,从而得![]() ,
,![]() ,计算
,计算![]() ,用
,用![]() ,
,![]() 代入
代入![]() 后得
后得![]() 的不等式,从而可求得
的不等式,从而可求得![]() 的范围.
的范围.
试题解析:(Ⅰ)由题意知:![]() ,
,![]()
![]()
![]()
![]()
![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆,其轨迹方程为
为焦点的椭圆,其轨迹方程为![]() …………………4分
…………………4分
(Ⅱ)设![]() ,
,![]() ,则将直线与椭圆的方程联立得:
,则将直线与椭圆的方程联立得: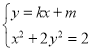 ,消去
,消去![]() ,得:
,得:![]() ,
,![]() ,
,![]() ………①
………①
![]() ,
,![]() …………………6分
…………………6分
![]() 原点
原点![]() 总在以
总在以![]() 为直径的圆的内部
为直径的圆的内部![]()
![]() 即
即![]() ……7分
……7分
而![]()
![]()
![]() ……9分
……9分
即![]()
![]()
![]() ,且满足①式
,且满足①式![]() 的取值范围是
的取值范围是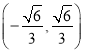 …12分
…12分

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目