题目内容
如图，正三棱柱ABC-A1B1C1的底面边长为a，侧棱长为
a，点D在棱A1C1上．(Ⅰ)若A1D=DC1，求证：直线BC1∥平面AB1D；
(Ⅱ)若
，二面角A1—AB1—D平面角的大小为θ，求tanθ的值．
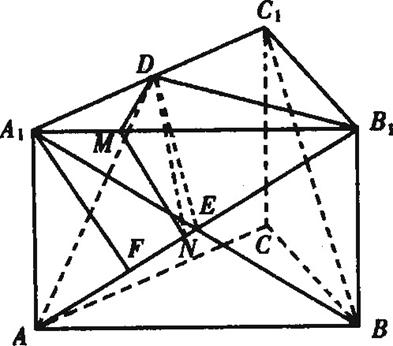
(Ⅰ)证明：连接A1B交AB1于E点，
在平行四边形ABB1A1中，
有A1E=BE，又A1D=DC1
∴DE为△A1BC1的中位线，从而DE∥BC1，又DE平面AB1D
∴直线BC1∥平面AB1D；
(Ⅱ)解：过D作DM⊥A1B1于M，则DM⊥平面A1ABB1，过M作MN⊥AB1于N，连接DN，
则∠MND为二面角A1-AB1-D的平面角θ，
∵,∴
,DM=
，
过A1作A1F⊥AB1于F，则A1F=
a，
=1-
MN=
，
∴tanθ=
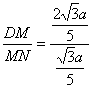=2．
练习册系列答案
相关题目
如图，正三棱柱ABC-A1B1C1各棱长都等于a，E是BB1的中点．
如图，正三棱柱ABC-A1B1C1的各棱长都2，E，F分别是AB，A1C1的中点，则EF的长是（ ）| A、2 | ||
B、
| ||
C、
| ||
D、
|
如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
（2013•郑州二模）如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
如图，正三棱柱ABC-A1B1C1中（注：底面为正三角形且侧棱与底面垂直），BC=CC1=2，P，Q分别为BB1，CC1的中点．