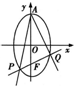题目内容
已知椭圆C:x2+
=1,过点M(0,1)的直线l与椭圆C相交于两点A、B.
(Ⅰ)若l与x轴相交于点P,且P为AM的中点,求直线l的方程;
(Ⅱ)设点N(0,
),求|
+
|的最大值.
| y2 |
| 4 |
(Ⅰ)若l与x轴相交于点P,且P为AM的中点,求直线l的方程;
(Ⅱ)设点N(0,
| 1 |
| 2 |
| NA |
| NB |
分析:(Ⅰ)设A(x1,y1),因为P为AM的中点,且P的纵坐标为0,M的纵坐标为1,所以y1=-1,又因为点A(x1,y1)在椭圆C上,所以x1=±
,由此能求出直线l的方程.
(Ⅱ)设A(x1,y1),B(x2,y2),则
=(x1,y1-
),
=(x2,y2-
),所以
+
=(x1+x2,y1+y2-1),则|
+
| =
,由此进行分类讨论,能推导出当直线AB的方程为x=0或y=1时,|
+
|有最大值1.
| ||
| 2 |
(Ⅱ)设A(x1,y1),B(x2,y2),则
| NA |
| 1 |
| 2 |
| NB |
| 1 |
| 2 |
| NA |
| NB |
| NA |
| NB |
| (x1+ x2)2+(y1+y2-1)2 |
| NA |
| NB |
解答:(Ⅰ)解:设A(x1,y1),
因为P为AM的中点,且P的纵坐标为0,M的纵坐标为1,
所以
=0,解得y1=-1,(1分)
又因为点A(x1,y1)在椭圆C上,
所以x12+
=1,即x12+
=1,解得x1=±
,
则点A的坐标为(
,-1)或(-
,-1),
所以直线l的方程为4
x-3y+3=0,或4
x+3y-3=0.
(Ⅱ)解:设A(x1,y1),B(x2,y2),
则
=(x1,y1-
),
=(x2,y2-
),
所以
+
=(x1+x2,y1+y2-1),
则|
+
| =
,
当直线AB的斜率不存在时,
其方程为x=0,A(0,2),B(0,-2),此时|
+
|=1;
当直线AB的斜率存在时,设其方程为y=kx+1,
由题设可得A、B的坐标是方程组
的解,
消去y得(4+k2)x2+2kx-3=0,
所以△=(2k)2+12(4+k2)>0,x1+x2=
,
则y1+y2=(kx1+1)+(kx2+1)=
,
所以|
+
|2=(
)2+(
-1)2
=
+1≤1,
当k=0时,等号成立,即此时|
+
|取得最大值1.
综上,当直线AB的方程为x=0或y=1时,|
+
|有最大值1.
因为P为AM的中点,且P的纵坐标为0,M的纵坐标为1,
所以
| y1+1 |
| 2 |
又因为点A(x1,y1)在椭圆C上,
所以x12+
| y12 |
| 4 |
| 1 |
| 4 |
| ||
| 2 |
则点A的坐标为(
| ||
| 2 |
| ||
| 2 |
所以直线l的方程为4
| 3 |
| 3 |
(Ⅱ)解:设A(x1,y1),B(x2,y2),
则
| NA |
| 1 |
| 2 |
| NB |
| 1 |
| 2 |
所以
| NA |
| NB |
则|
| NA |
| NB |
| (x1+ x2)2+(y1+y2-1)2 |
当直线AB的斜率不存在时,
其方程为x=0,A(0,2),B(0,-2),此时|
| NA |
| NB |
当直线AB的斜率存在时,设其方程为y=kx+1,
由题设可得A、B的坐标是方程组
|
消去y得(4+k2)x2+2kx-3=0,
所以△=(2k)2+12(4+k2)>0,x1+x2=
| -2k |
| 4+k2 |
则y1+y2=(kx1+1)+(kx2+1)=
| 8 |
| 4+k2 |
所以|
| NA |
| NB |
| -2k |
| 4+k2 |
| 8 |
| 4+k2 |
=
| -12k2 |
| (4+ k2)2 |
当k=0时,等号成立,即此时|
| NA |
| NB |
综上,当直线AB的方程为x=0或y=1时,|
| NA |
| NB |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答,注意分类讨论思想的灵活运用.

练习册系列答案
相关题目
 如图所示,已知椭圆C:
如图所示,已知椭圆C: