题目内容

如图所示,已知△ABC的三个顶点都不在平面α内,它的三边AB、BC、AC延长后分别交平面α于点P、Q、R.求证:点P、Q、R在同一条直线上.

解析:要证三点共线,可考虑证明这三点是两个相交平面的公共点.

证明:由已知AB的延长线交平面α于点P,根据公理2平面ABC与平面α必相交于一条直线,设为l.

∵P∈直线AB,∴P∈面ABC.

    又直线AB∩面α=P,∴P∈面α.

∴P是面ABC与面α的公共点.∵面ABC∩面α=l,∴P∈l.

    同理,Q∈l,R∈l.∴点P、Q、R在同一条直线l上.

点评:本题主要考查诸点共线的证明方法,即转化为平面相交的问题.要求先由两点确定直线,再判断其他点在该直线上.切记找出平面的交线.

练习册系列答案
相关题目
4、如图所示，已知AB⊥平面BCD，BC⊥CD，则图中互相垂直的平面有（　　）
如图所示，已知AB⊥平面BCD，M、N分别是AC、AD的中点，BC⊥CD．
（1）求证：MN∥平面BCD；
（2）求证：平面BCD⊥平面ABC；
（3）若AB=1，BC=
3
，求直线AC与平面BCD所成的角．
A：如图所示，已知AB为⊙O的直径，AC为弦，OD∥BC，交AC于点D，BC=4cm，
（1）试判断OD与AC的关系；
（2）求OD的长；
（3）若2sinA-1=0，求⊙O的直径．
B：（选修4-4）已知直线l经过点P（1，1），倾斜角α=
3π4
．
（1）写出直线l的参数方程；
（2）设l与圆x2+y2=4相交于两点A、B，求点P到A、B两点的距离之积．
一次机器人足球比赛中，甲队1号机器人由点A开始作匀速直线运动，到达点B时，发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动．如图所示，已知AB=4
2
dm，AD=17dm，∠BAC=45°．若忽略机器人原地旋转所需的时间，则该机器人最快可在何处截住足球？
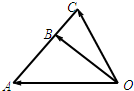精英家教网如图所示，已知
AB
=2
BC
，
OA
=
a
，
OB
=
b
，
OC
=
c
，则
c
=
 
．（用
a
，
b
表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网