题目内容
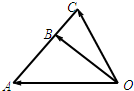如图所示，已知| AB |
| BC |
| OA |
| a |
| OB |
| b |
| OC |
| c |
| c |
| a |
| b |
分析：利用向量的加法法则和减法法则，将
，
分别用向量
，
，
表示，即可得到答案．
| AB |
| BC |
| OA |
| OB |
| OC |
解答：解：∵
=2
，
∴
-
=2(
-
)，
整理可得，
=
-
，
又∵
=
，
=
，
=
，
∴
=
-
．
故答案为：
-
．
| AB |
| BC |
∴
| OB |
| OA |
| OC |
| OB |
整理可得，
| OC |
| 3 |
| 2 |
| OB |
| 1 |
| 2 |
| OA |
又∵
| OA |
| a |
| OB |
| b |
| OC |
| c |
∴
| c |
| 3 |
| 2 |
| b |
| 1 |
| 2 |
| a |
故答案为：
| 3 |
| 2 |
| b |
| 1 |
| 2 |
| a |
点评：本题考查了向量的加法和向量的减法运算，解题的关键是将未知的向量向已知的向量去转化，解题时注意加法要“首尾连”，减法是“共起点”．属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图所示，已知AB⊥平面BCD，M、N分别是AC、AD的中点，BC⊥CD．
A：如图所示，已知AB为⊙O的直径，AC为弦，OD∥BC，交AC于点D，BC=4cm，
一次机器人足球比赛中，甲队1号机器人由点A开始作匀速直线运动，到达点B时，发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动．如图所示，已知