题目内容
【题目】已知椭圆C: ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]() .
.
(Ⅰ)求椭圆C的方程;

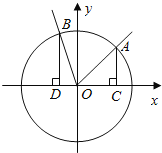
(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点,过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、![]() ,证明
,证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
【答案】(Ⅰ) ![]() ;(Ⅱ)(i)证明见解析;(ii)
;(Ⅱ)(i)证明见解析;(ii) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意可得![]() ,椭圆C的方程为
,椭圆C的方程为![]() .
.
(Ⅱ)(i)设![]() ,由题意可得
,由题意可得![]() ,结合斜率公式可得PM的斜率
,结合斜率公式可得PM的斜率![]() ,QM的斜率
,QM的斜率![]() ,故
,故![]() 为定值-3.
为定值-3.
(ii)设![]() ,直线PA的方程为
,直线PA的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() .则
.则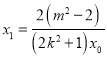 ,
,  ,同理
,同理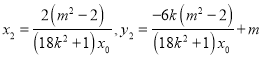 ,故
,故![]() .结合均值不等式的结论可得当且仅当
.结合均值不等式的结论可得当且仅当![]() 时,直线AB的斜率有最小值为
时,直线AB的斜率有最小值为![]() .
.
试题解析:
(Ⅰ)设椭圆的半焦距为c,
由题意知![]() ,
,
所以![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)(i)设![]() ,
,
由![]() ,可得
,可得![]() ,
,
所以直线PM的斜率![]() ,
,
直线QM的斜率![]() ,
,
此时![]() ,所以
,所以![]() 为定值-3.
为定值-3.
(ii)设![]() ,
,
直线PA的方程为![]() ,
,
直线QB的方程为![]() ,
,
联立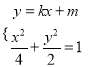 ,
,
整理得![]() .
.
由![]() 可得
可得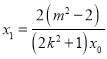 ,
,
所以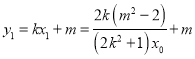 ,
,
同理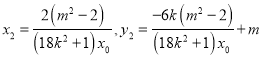 ,
,
所以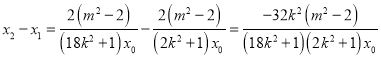 ,
,
 ,
,
所以![]() .
.
由![]() ,可知
,可知![]() ,
,
所以![]() ,等号当且仅当
,等号当且仅当![]() 时取得,
时取得,
此时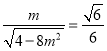 ,即
,即![]() ,符合题意,
,符合题意,
所以直线AB的斜率的最小值为![]() .
.

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.