题目内容
函数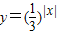
的值域是 ．
【答案】分析：化已知函数为分段函数，分别由指数函数的单调性可得值域，综合可得．
解答：解：由题意可得y=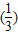
|x|=
，
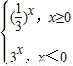由指数函数y=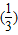
x单调递减可知，
当x≥0时，0＜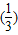
x≤
=1，
故0＜y≤1；
同理由指数函数y=3x单调递增可知，
当x＜0时，0＜3x＜3=1，
故0＜y＜1；
综上可知：函数的值域为{y|0＜y≤1}
故答案为：{y|0＜y≤1}．
点评：本题考查函数的值域，涉及指数函数以及分段函数的值域，属基础题．
解答：解：由题意可得y=
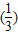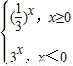|x|=，由指数函数y=
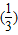x单调递减可知，当x≥0时，0＜
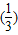x≤=1，故0＜y≤1；
同理由指数函数y=3x单调递增可知，
当x＜0时，0＜3x＜3=1，
故0＜y＜1；
综上可知：函数的值域为{y|0＜y≤1}
故答案为：{y|0＜y≤1}．
点评：本题考查函数的值域，涉及指数函数以及分段函数的值域，属基础题．
练习册系列答案
相关题目
（2012•海淀区二模）某同学为研究函数