题目内容
已知在数列{an}中,Sn是它的前n项和,且Sn+1=4an+2(n=1,2,.…),a1=1。
(1)设bn=an+1-2an(n=1,2,…),求证:数列{bn}是等比数列;
(2)设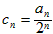 ,求证:数列{cn}是等差数列。
,求证:数列{cn}是等差数列。
(1)设bn=an+1-2an(n=1,2,…),求证:数列{bn}是等比数列;
(2)设
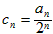 ,求证:数列{cn}是等差数列。
,求证:数列{cn}是等差数列。 证明:(1)∵Sn+1=4an+2,
∴Sn+2=4an+1+2,两式相减,
得Sn+2-Sn+1=4an+1-4an(n=1,2,3…),
即an+2=4an+1-4an,
变形得an+2-2an+1=2(an+1-2an),
∵bn=an+1-2an(n=1,2,…),
∴bn+1=2bn,
由S2=a1+a2=4a1+2,a1=1,
得a2=5,b1=a2-2a1=3,
由此可知,数列{bn}是首项为3,公比为2的等比数列,故bn=3·2n-1;
(2)∵
∴
将bn=3·2n-1代入得
由此可知,数列{cn}是公差为 的等差数列,
的等差数列,
它的首项c1 ,
,
故 。
。
∴Sn+2=4an+1+2,两式相减,
得Sn+2-Sn+1=4an+1-4an(n=1,2,3…),
即an+2=4an+1-4an,
变形得an+2-2an+1=2(an+1-2an),
∵bn=an+1-2an(n=1,2,…),
∴bn+1=2bn,
由S2=a1+a2=4a1+2,a1=1,
得a2=5,b1=a2-2a1=3,
由此可知,数列{bn}是首项为3,公比为2的等比数列,故bn=3·2n-1;
(2)∵

∴

将bn=3·2n-1代入得

由此可知,数列{cn}是公差为
 的等差数列,
的等差数列,它的首项c1
 ,
,故
 。
。 
练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目