题目内容
如图所示，双曲线的中心在坐标原点，焦点在x轴上，F1，F2分别为左、右焦点，双曲线的左支上有一点P，∠F1PF2=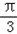
，且△PF1F2的面积为2
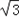，又双曲线的离心率为2，求该双曲线的方程．
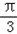，且△PF1F2的面积为2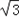，又双曲线的离心率为2，求该双曲线的方程．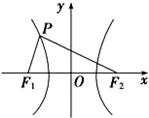
解：设双曲线方程为：
﹣
=1（a＞0，b＞0），
F1（﹣c，0），F2（c，0），P（x0，y0）．
在△PF1F2中，由余弦定理，得：
|F1F2|2=|PF1|2+|PF2|2﹣2
|PF1|
|PF2|
cos
=（|PF1|﹣|PF2|）2+|PF1|
|PF2|．
即4c2=4a2+|PF1|
|PF2|．
又∵
=2
．
∴
|PF1|
|PF2|
sin
=2
．
∴|PF1|
|PF2|=8．
∴4c2=4a2+8，即b2=2．
又∵e=
=2，
∴a2=
．
∴双曲线的方程为：
﹣
=1．
﹣=1（a＞0，b＞0），F1（﹣c，0），F2（c，0），P（x0，y0）．
在△PF1F2中，由余弦定理，得：
|F1F2|2=|PF1|2+|PF2|2﹣2
|PF1||PF2|cos=（|PF1|﹣|PF2|）2+|PF1||PF2|．即4c2=4a2+|PF1|
|PF2|．又∵
=2．∴
|PF1||PF2|sin=2．∴|PF1|
|PF2|=8．∴4c2=4a2+8，即b2=2．
又∵e=
=2，∴a2=
．∴双曲线的方程为：
﹣=1．
练习册系列答案
相关题目
（2012•红桥区一模）如图所示，双曲线
（2008•宣武区一模）在面积为9的△ABC中，
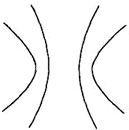已知定圆O1、O2的半径分别为r1、r2，圆心距|O1O2|=2，动圆C与圆O1、O2都相切，圆心C的轨迹为如图所示的两条双曲线，两条双曲线的离心率分别为e1、e2，则| e1+e2 |
| e1e2 |
| A、r1+r2 |
| B、r1和r2中的较大者 |
| C、r1和r2中的较小者 |
| D、|r1-r2| |
中，
，且
。现建立以A点为坐标原点，以
的平分线所在直线为x轴的平面直角坐标系，如图所示。
的值。