Question

设函数f（x）=

3-cos2x

2

-4t•sin

x

2

cos

x

2

+2t²-6t（x∈R），其中t∈R，将f（x）的最小值记为g（t）．
（1）求g（t）的表达式；
（2）当-1≤t≤1时，要使关于t的方程g（t）=kt有且仅有一个实根，求实数k的取值范围．

Answer 1

考点：三角函数的最值,根的存在性及根的个数判断,三角函数中的恒等变换应用

专题：三角函数的求值

分析：（1）利用二倍角公式化简函数的解析式为f（x）=（sinx-t）²+t²-6t+1．再分当t＜-1时、当-1≤t≤1时、当t＞1时三种情况，分别求得g（t）的解析式，可得结论．
（2）由题意可得函数g（t）的图象在区间[-1，1]上和直线y=kt只有一个交点，如图，求得OA的斜率，OC的斜率，可得k的范围．

解答： 解：（1）函数f（x）=

3-cos2x

2

-4t•sin

x

2

cos

x

2

+2t²-6t
=sin²x-2tsinx+2t²-6t+1
=（sinx-t）²+t²-6t+1．
当t＜-1时，g（t）=（-1-t）²+t²-6t+1=2t²-4t+2．
当-1≤t≤1时，g（t）=t²-6t+1．
当t＞1时，g（t）=（1-t）²+t²-6t+1=2t²-8t+2．
综上可得，g（t）=

2t2-4t+2，t＜-1 t2-6t+1，-1≤t≤1 2t2-8t+2，t＞1

．
（2）当-1≤t≤1时，要使关于t的方程g（t）=kt有
且仅有一个实根，
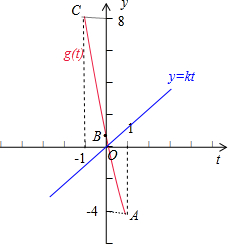
则函数g（t）的图象（红线部分）在区间[-1，1]上和直线y=kt（蓝线）只有一个交点，
如图所示：
再根据OA的斜率为

-4-0

1-0

=-4，OC的斜率为

8-0

-1-0

=-8，可得k≥-4，或 k≤-8．

点评：本题主要考查二倍角公式、二次函数的性质，方程根的存在性及个数判断，属于基础题．